题目内容
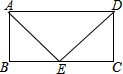 如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为
如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为考点:矩形的性质
专题:
分析:由矩形ABCD中,E是BC的中点,易得△ABE≌△DCE,又由∠AED=90°,可证得△ADE,△ABE是等腰直角三角形,即可得AB=BE=
AD.
| 1 |
| 2 |
解答:解:∵矩形ABCD中,E是BC的中点,
∴AB=CD,BE=CE,∠B=∠C=90°,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS),
∴AE=DE,
∵∠AED=90°,
∴∠DAE=45°,
∴∠BAE=90°-∠DAE=45°,
∴∠BEA=∠BAE=45°,
∴AB=BE=
AD=
×10=5.
故答案为:5.
∴AB=CD,BE=CE,∠B=∠C=90°,
在△ABE和△DCE中,
|
∴△ABE≌△DCE(SAS),
∴AE=DE,
∵∠AED=90°,
∴∠DAE=45°,
∴∠BAE=90°-∠DAE=45°,
∴∠BEA=∠BAE=45°,
∴AB=BE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:5.
点评:此题考查了矩形的性质以及等腰直角三角形的判定与性质,关键是正确证明∠DAE=45°,AB=BE=
AD.
| 1 |
| 2 |

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8,CD=3,则⊙O的半径为( )
如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8,CD=3,则⊙O的半径为( )| A、4 | ||
| B、5 | ||
C、
| ||
D、
|
二次函数y=3x2+mx+6的图象过点A(-3,0),则m的值是( )
| A、3 | B、9 | C、11 | D、-11 |
 一个长方体的主视图与俯视图如图所示,则这个长方体的表面积是
一个长方体的主视图与俯视图如图所示,则这个长方体的表面积是 如图,已知点E,C在线段BF上,BE=CF,请在下列四个等式中,选出两个作为条件,推出△ABC≌△DEF,并予以证明
如图,已知点E,C在线段BF上,BE=CF,请在下列四个等式中,选出两个作为条件,推出△ABC≌△DEF,并予以证明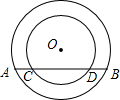 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于点C,D.
如图,两个圆都以点O为圆心,大圆的弦AB交小圆于点C,D.