题目内容
13.解方程(1)7x(5x+2)=6(5x+2)
(2)4x2-8x+1=0.
分析 (1)因式分解法求解可得;
(2)公式法求解可得.
解答 解:(1)∵7x(5x+2)-6(5x+2)=0,
∴(5x+2)(7x-6)=0,
∴5x+2=0或7x-6=0,
解得:x=-$\frac{2}{5}$或x=$\frac{6}{7}$;
(2)∵a=4,b=-8,c=1,
∴△=64-4×4×1=48>0,
则x=$\frac{8±4\sqrt{3}}{8}$=$\frac{2±\sqrt{3}}{2}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.在解方程$\frac{x-1}{2}$=1-$\frac{2x+3}{3}$时,去分母正确的是( )
| A. | 3(x-1)=1-2(2+3x) | B. | 3(x-1)=1+2(2x+3) | C. | 3(x-1)=6-2(2x+3) | D. | 3(x-1)=6+2(2x+3) |
18.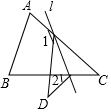 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )| A. | 140° | B. | 90° | C. | 80° | D. | 40° |
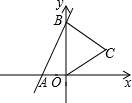 如图,直线y=3x+6与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为(-1,3).
如图,直线y=3x+6与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为(-1,3).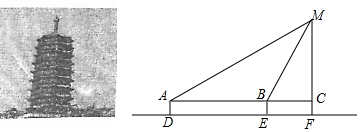
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.