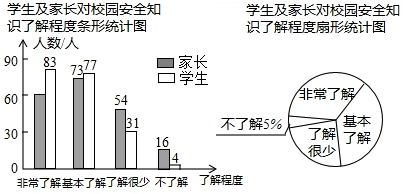
题目内容
18.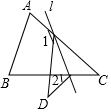 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )| A. | 140° | B. | 90° | C. | 80° | D. | 40° |
分析 由折叠的性质得到∠D=∠C,再利用外角性质即可求出所求角的度数.
解答  解:由折叠的性质得:∠D=∠C=40°,
解:由折叠的性质得:∠D=∠C=40°,
根据外角性质得:∠1=∠3+∠C,∠3=∠2+∠D,
则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+80°,
则∠1-∠2=80°.
故选C.
点评 此题考查了翻折变换(折叠问题)以及外角性质,熟练掌握折叠的性质是解本题的关键.

练习册系列答案
相关题目
6.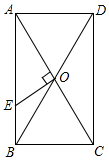 如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
 如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )| A. | AE=5 | B. | ∠BOE=∠BCE | C. | CE⊥OB | D. | sin∠BOE=$\frac{3}{5}$ |
3.下列四组线段中,可以构成直角三角形的是( )
| A. | 1.5,2,3 | B. | 4,5,5 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,1 |
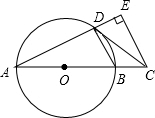 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.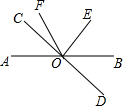 如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数.
如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数.