题目内容
2. 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax-1与线段AB交于点P,直接写出a的取值范围.
分析 (1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数解析式;
(2)由点B在反比例函数图象上可得出mn=2,再根据三角形的面积公式结合△ABC面积为2,即可求出m值,利用反比例函数图象上点的坐标特征即可求出点B的坐标;
(3)分别将点A、B的坐标代入直线y=ax-1中求出a的临界值,由此即可得出a的取值范围.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$的图象经过点A(1,2),
∴k=1×2=2,
∴反比例函数解析式为y=$\frac{2}{x}$.
(2)∵点B(m,n)在反比例函数y=$\frac{2}{x}$的图象上,
∴mn=2.
又∵S△ABC=$\frac{1}{2}$BC•(yA-yB)=$\frac{1}{2}$m(2-n)=m-$\frac{1}{2}$mn=m-1=2,
∴m=3,n=$\frac{2}{3}$,
∴点B的坐标为(3,$\frac{2}{3}$).
(3)将A(1,2)代入y=ax-1中,
2=a-1,解得:a=3;
将B(3,$\frac{2}{3}$)代入y=ax-1中,
$\frac{2}{3}$=3a-1,解得:a=$\frac{5}{9}$.
∵直线y=ax-1与线段AB交于点P,P为线段AB上一动点(P不与A、B重合),
∴$\frac{5}{9}$<a<3.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及一次函数图象上点的坐标特征,根据点的坐标特征利用反比例(一次)函数图象上点的坐标特征找出反比例(一次)函数解析式是解题的关键.

练习册系列答案
相关题目
12.多项式5x2-8x+1+x2+7x-6x2是( )
| A. | 一次二项式 | B. | 二次六项式 | C. | 二次二项式 | D. | 二次三项式 |
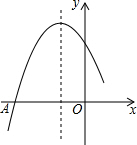 如图是二次函数y=ax2+bx+c的图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①c>0;②b2>4ac;③b=-2a;④a+b+c=0,其中正确结论的番号是①②④.
如图是二次函数y=ax2+bx+c的图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①c>0;②b2>4ac;③b=-2a;④a+b+c=0,其中正确结论的番号是①②④.