题目内容
9.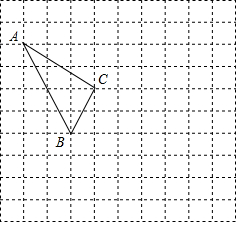 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标;
(4)计算△A′B′C′的周长﹒
分析 (1)根据A、C两点的坐标建立平面直角坐标系即可;
(2)分别作出各点关于y轴的对称点,再顺次连接即可;
(3)根据B′在坐标系中的位置写出其坐标即可;
(4)利用勾股定理求出△A′B′C′的边长,进而可得出结论.
解答 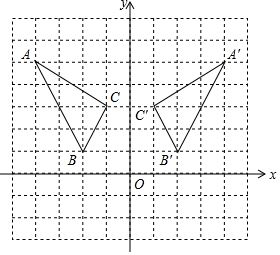 解:(1)如图;
解:(1)如图;
(2)如图,△A′B′C′即为所求;
(3)由图可知,B′(2,1);
(4)∵A′B′=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,A′C′=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,B′C′=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴△A′B′C′的周长=2$\sqrt{5}$+$\sqrt{13}$+$\sqrt{5}$=3$\sqrt{5}$+$\sqrt{13}$.
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
17.“水是生命之源”,某城市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
(1)如果某用户1月份用水量为19m3,那么该用户1月份应该缴纳水费多少元.
(2)如果某用户2月份共缴纳水费80元,那么该用户2月份用水多少立方米?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,那么该用户3月份实际应该缴纳水费多少元?
| 用水量/月 | 单价(元/m3) |
| 不超过20m3 | 3 |
| 超过20m3的部分 | 4 |
| 另:每立方米用水加收0.2元的城市污水处理费 | |
(2)如果某用户2月份共缴纳水费80元,那么该用户2月份用水多少立方米?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,那么该用户3月份实际应该缴纳水费多少元?
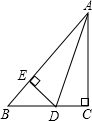 如图,△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于E,测得BC=9,BD=6,则DE的长是( )
如图,△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于E,测得BC=9,BD=6,则DE的长是( ) 如图,点A是抛物线y=x2-4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为(2,-1)或(2,2).
如图,点A是抛物线y=x2-4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为(2,-1)或(2,2).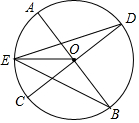 如图,已知,AB、CD是⊙O的两条直径,E为$\widehat{AC}$的中点,求证:EO平分∠DEB.
如图,已知,AB、CD是⊙O的两条直径,E为$\widehat{AC}$的中点,求证:EO平分∠DEB. 如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点.将△ACD绕点C逆时针旋转90°到△BCE.
如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点.将△ACD绕点C逆时针旋转90°到△BCE.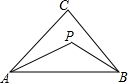 如图,P是△ABC内一点,求证:∠APB>∠ACB.
如图,P是△ABC内一点,求证:∠APB>∠ACB.