题目内容
14．
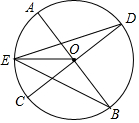如图，已知，AB、CD是⊙O的两条直径，E为$\widehat{AC}$的中点，求证：EO平分∠DEB．
分析 过O作ON⊥DE于N，OM⊥BE于M，根据已知条件得到$\widehat{DE}$=$\widehat{BE}$，得到DE=BE，推出ON=OM，根据角平分线的判定定理即可得到结论．
解答 
证明：过O作ON⊥DE于N，OM⊥BE于M，
∵∠AOD=∠BOC，
∴$\widehat{AD}$=$\widehat{BC}$，
∵E为$\widehat{AC}$的中点，
∴$\widehat{DE}$=$\widehat{BE}$，
∴DE=BE，
∴ON=OM，
∴EO平分∠DEB．
点评 本题考查了圆周角，弧，弦的关系，角平分线的性质，正确的作出辅助线是解题的关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
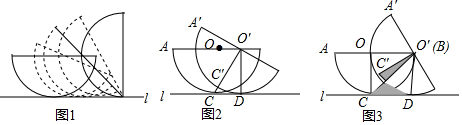如图1，一个半径为2的半圆在平面作无滑动顺时针滚动，可以把平面看做直线l，初始位置的半圆O与直线l相切于点C，AB∥l，滚动过程中，半圆O′与直线l相切于点D，点A、B、C在半圆O′上的对应点分别为A′、B′、C′．
如图，在平面直角坐标系xOy中，正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A，B两点，A点的横坐标为2，AC⊥x轴于点C，连接BC．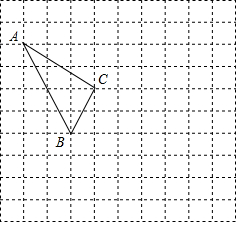
在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）．
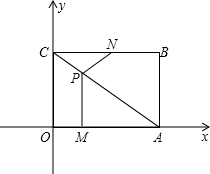如图，平面直角坐标系中，四边形OABC为矩形，点A，B的坐标分别为（4，0），（4，3），动点M，N分别从O，B同时出发．以每秒1个单位的速度运动．其中，点M沿OA向终点A运动，点N沿BC向终点C运动．其中，点M沿OA向终点A运动，点N沿BN向终点C运动．过点M作MP⊥OA，交AC于P，连接NP，设M、N运动的时间为t秒（0＜t＜4）．
如图．已知二次函数y=ax2+bx（α≠0）经过点A（-2，0），B（-3，3）．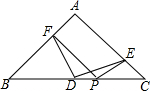
如图，Rt△ABC中，∠BAC=90°，AB=AC，D为BC的中点，P为BC上一点，PF⊥AB于F，PE⊥AC于E，则DF与DE的关系为DF=DE且DF⊥ED．