题目内容
4.化简求值:$\frac{2}{3}$$\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$(其中x是方程y2-3y-4=0的一个解)分析 先解方程y2-3y-4=0,求出y1=-1,y2=4.再根据二次根式的性质得出x≥0,那么x=4.然后化简$\frac{2}{3}$$\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$,再代入计算即可.
解答 解:解方程y2-3y-4=0,
(y+1)(y-4)=0,
y1=-1,y2=4.
∵9x≥0,
∴x≥0,
∴x=4.
当x=4时,
$\frac{2}{3}$$\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$
=2$\sqrt{x}$+3$\sqrt{x}$-2$\sqrt{x}$
=3$\sqrt{x}$
=3×$\sqrt{4}$
=3×2
=6.
点评 本题考查了一元二次方程的解法,二次根式的化简求值,确定x的值是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
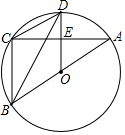 如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且OD⊥AC于点E,连结BD、CD.
如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且OD⊥AC于点E,连结BD、CD.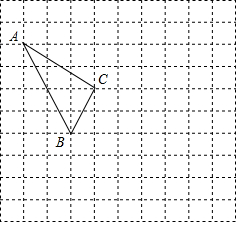 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
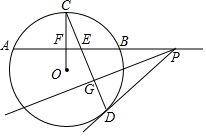 如图,在⊙O中,OC⊥AB于点F,弦CD交弦AB于点E,线段ED的垂直平分线GP交AB延长线于点P,连结PD.
如图,在⊙O中,OC⊥AB于点F,弦CD交弦AB于点E,线段ED的垂直平分线GP交AB延长线于点P,连结PD.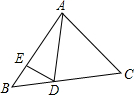 如图,△ABC中,D、E分别是BC、AB边上的点,AD平分∠EDC,试说明∠BED>∠B的道理.
如图,△ABC中,D、E分别是BC、AB边上的点,AD平分∠EDC,试说明∠BED>∠B的道理.