题目内容
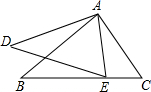 如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是( )
如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是( )| A、∠B=∠D | ||||
| B、∠C=∠AED | ||||
C、
| ||||
D、
|
考点:相似三角形的判定
专题:
分析:根据已知及相似三角形的判定方法对各个选项进行分析,从而得到最后答案.
解答:解:∵∠BAD=∠CAE,
∴∠DAE=∠BAC,
∴A,B,D都可判定△ABC∽△ADE
选项C中不是夹这两个角的边,所以不相似,
故选:C.
∴∠DAE=∠BAC,
∴A,B,D都可判定△ABC∽△ADE
选项C中不是夹这两个角的边,所以不相似,
故选:C.
点评:此题考查了相似三角形的判定:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.

练习册系列答案
相关题目
抛物线y=2x2,y=-2x2,y=
x2共有的性质是( )
| 1 |
| 2 |
| A、开口向下 |
| B、对称轴是y轴 |
| C、都有最低点 |
| D、y的值随x的增大而减小 |
下列运算中,不正确的是( )
| A、(-a3)2=a9 |
| B、a3+a3=2a3 |
| C、a2•a3=a5 |
| D、2a3÷a2=2a |
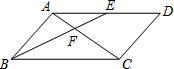 已知:如图,?ABCD中,E是AD中点,BE交AC于点F,设
已知:如图,?ABCD中,E是AD中点,BE交AC于点F,设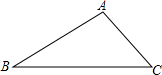 如图,在△ABC中,AB=8,∠ABC=30°,∠ACB=45°,则BC的长为
如图,在△ABC中,AB=8,∠ABC=30°,∠ACB=45°,则BC的长为 如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.