题目内容
 如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.(1)求证:PD∥AB;
(2)求证:DE=BF;
(3)若AC=6,tan∠CAB=
| 4 |
| 3 |
考点:圆的综合题
专题:
分析:(1)连结OD,由AB为⊙O的直径,根据圆周角定理得AB为⊙O的直径得∠ACB=90°,再由ACD=∠BCD=45°,则∠DAB=∠ABD=45°,所以△DAB为等腰直角三角形,所以DO⊥AB,根据切线的性质得OD⊥PD,于是可得到DP∥AB;
(2)利用角的关系得出∠FBD=∠EDA,进而得出△FBD≌△EDA,即可得出DE=BF;
(3)在Rt△ACB中,利用AC=6,tan∠CAB=
,可得BC=8,再利用勾股定理得出AB=10,由△DAB为等腰直角三角形,可得AD=5
,由AE⊥CD,得出△ACE为等腰直角三角形,得出AE=CE=3
,在Rt△AED中,可得DE=4
,得出CD=7
,由角的关系得出△PDA∽△PCD,利用比例式可得出PA=
PD,PC=
PD,由PC=PA+AC,可求得PD=
,即可得出 PC的值.
(2)利用角的关系得出∠FBD=∠EDA,进而得出△FBD≌△EDA,即可得出DE=BF;
(3)在Rt△ACB中,利用AC=6,tan∠CAB=
| 4 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
| 5 |
| 7 |
| 7 |
| 5 |
| 35 |
| 4 |
解答:证明:(1)连结OD,如图,

∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°,
∴∠DAB=∠ABD=45°,
∴△DAB为等腰直角三角形,
∴DO⊥AB,
∵PD为⊙O的切线,
∴OD⊥PD,
∴DP∥AB;
(2)∵AE⊥CD于点E,BF⊥CD,
∴AE∥BF,
∴∠FBO=∠EAO,
∵△DAB为等腰直角三角形,
∴∠FBD+∠EAD=90°,
∵∠EDA+∠∠EAD=90°,
∴∠FBD=∠EDA
在△FBD和△EDA中,
,
∴△FBD≌△EDA(AAS)
∴DE=BF.
(3)在Rt△ACB中,
∵AC=6,tan∠CAB=
,
∴BC=6×
=8,
∴AB=
=
=10,
∵△DAB为等腰直角三角形,
∴AD=
=5
,
∵AE⊥CD,
∴△ACE为等腰直角三角形,
∴AE=CE=
=
=3
,
在Rt△AED中,DE=
=4
,
∴CD=CE+DE=3
+4
=7
,
∵AB∥PD,
∴∠PDA=∠DAB=45°,
∴∠PDA=∠PCD,
又∵∠DPA=∠CPD,
∴△PDA∽△PCD,
∴
=
=
=
,
∴PA=
PD,PC=
PD,
又∵PC=PA+AC,
∴
PD+6=
PD,解得PD=
,
∴PC=
PD+6=
×
+6=
+6=
.

∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°,
∴∠DAB=∠ABD=45°,
∴△DAB为等腰直角三角形,
∴DO⊥AB,
∵PD为⊙O的切线,
∴OD⊥PD,
∴DP∥AB;
(2)∵AE⊥CD于点E,BF⊥CD,
∴AE∥BF,
∴∠FBO=∠EAO,
∵△DAB为等腰直角三角形,
∴∠FBD+∠EAD=90°,
∵∠EDA+∠∠EAD=90°,
∴∠FBD=∠EDA
在△FBD和△EDA中,
|
∴△FBD≌△EDA(AAS)
∴DE=BF.
(3)在Rt△ACB中,
∵AC=6,tan∠CAB=
| 4 |
| 3 |
∴BC=6×
| 4 |
| 3 |
∴AB=
| AC2+BC2 |
| 62+82 |
∵△DAB为等腰直角三角形,
∴AD=
| AB | ||
|
| 2 |
∵AE⊥CD,
∴△ACE为等腰直角三角形,
∴AE=CE=
| AC | ||
|
| 6 | ||
|
| 2 |
在Rt△AED中,DE=
| AD2-AE2 |
| 2 |
∴CD=CE+DE=3
| 2 |
| 2 |
| 2 |
∵AB∥PD,
∴∠PDA=∠DAB=45°,
∴∠PDA=∠PCD,
又∵∠DPA=∠CPD,
∴△PDA∽△PCD,
∴
| PD |
| PC |
| PA |
| PD |
| AD |
| CD |
5
| ||
7
|
∴PA=
| 5 |
| 7 |
| 7 |
| 5 |
又∵PC=PA+AC,
∴
| 5 |
| 7 |
| 7 |
| 5 |
| 35 |
| 4 |
∴PC=
| 5 |
| 7 |
| 5 |
| 7 |
| 35 |
| 4 |
| 25 |
| 4 |
| 49 |
| 4 |
点评:本题主要考查了圆的综合题,切线的性质,三角形全等及相似的知识,解题的关键是利用相似三角形得出边的关系,再列出算式求解.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
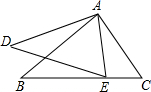 如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是( )
如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是( )| A、∠B=∠D | ||||
| B、∠C=∠AED | ||||
C、
| ||||
D、
|
在Rt△ABC中,∠ACB=90°,BC=1,AC=2,则下列结论正确的是( )
A、sinA=
| ||||
B、tanA=
| ||||
C、cosB=
| ||||
D、tanB=
|
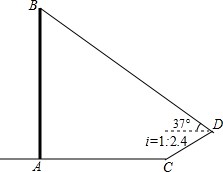 如图,高压电线杆AB垂直地面,测得电线杆AB的底部A到斜坡C的水平距离AC长为15.2米,落在斜坡上的电线杆的影长CD为5.2米,在D点处测得电线杆顶B的仰角为37°.已知斜坡CD的坡比i=1:2.4,求该电线杆AB的高.(参考数据:sin37°=0.6)
如图,高压电线杆AB垂直地面,测得电线杆AB的底部A到斜坡C的水平距离AC长为15.2米,落在斜坡上的电线杆的影长CD为5.2米,在D点处测得电线杆顶B的仰角为37°.已知斜坡CD的坡比i=1:2.4,求该电线杆AB的高.(参考数据:sin37°=0.6)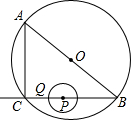 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆,设点Q运动的时间为ts.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆,设点Q运动的时间为ts. 如图,如果某个斜坡AB的长度为10米,且该斜坡最高点A到地面BC的铅垂高度为8米,那么该斜坡的坡比是
如图,如果某个斜坡AB的长度为10米,且该斜坡最高点A到地面BC的铅垂高度为8米,那么该斜坡的坡比是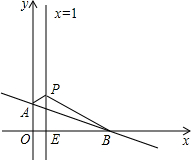 如图,平面直角坐标系中,直线AB:y=-
如图,平面直角坐标系中,直线AB:y=-