题目内容
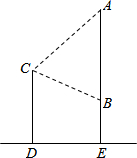如图所示，小明站在地面上照镜子，镜子AB挂在和地面垂直的墙面AE上，镜子的高度AB为（1+
| ||
| 3 |
| 3 |
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：过点C作CG⊥AE于点G，由四边形DEGC是矩形，得出GE=CD=1.2米，设BE=x米，则BG=（1.2-x）米，AG=（1+
）-（1.2-x）=（
-0.2+x）米．在Rt△BCG中由锐角三角函数的定义得出CG=
=
=
（1.2-x），同理，在Rt△ACG中，由锐角三角函数的定义得出CG=
=
-0.2+x，
进而列出方程
（1.2-x）=
-0.2+x，解方程即可求解．
| ||
| 3 |
| ||
| 3 |
| BG |
| tan∠BCG |
| 1.2-x | ||||
|
| 3 |
| AG |
| tan∠ACG |
| ||
| 3 |
进而列出方程
| 3 |
| ||
| 3 |
解答：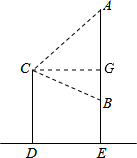
解：如图，过点C作CG⊥AE于点G，四边形DEGC是矩形，GE=CD=1.2米，
设BE=x米，则BG=（1.2-x）米，AG=（1+
）-（1.2-x）=（
-0.2+x）米．
在Rt△BCG中，∵∠BCG=30°，BG=（1.2-x）米，
∴CG=
=
=
（1.2-x），
同理，在Rt△ACG中，∵∠ACG=60°，AG=（
-0.2+x）米，
∴CG=
=
-0.2+x，
∴
（1.2-x）=
-0.2+x，
∴解得x=
≈1.03．
答：镜子底端离地面的距离约为1.03米．
解：如图，过点C作CG⊥AE于点G，四边形DEGC是矩形，GE=CD=1.2米，设BE=x米，则BG=（1.2-x）米，AG=（1+
| ||
| 3 |
| ||
| 3 |
在Rt△BCG中，∵∠BCG=30°，BG=（1.2-x）米，
∴CG=
| BG |
| tan∠BCG |
| 1.2-x | ||||
|
| 3 |
同理，在Rt△ACG中，∵∠ACG=60°，AG=（
| ||
| 3 |
∴CG=
| AG |
| tan∠ACG |
| ||
| 3 |
∴
| 3 |
| ||
| 3 |
∴解得x=
12-
| ||
| 10 |
答：镜子底端离地面的距离约为1.03米．
点评：此题主要考查了解直角三角形的应用-仰角俯角问题，准确作出辅助线构造直角三角形，从而利用锐角三角函数关系列出方程是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
要使代数式
的值小于2x-7，则x的取值范围是（ ）
| 6-3x |
| 3 |
| A、x＞-3 | ||
| B、x＜3 | ||
| C、x＞3 | ||
D、x＞
|
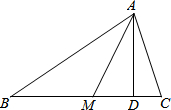如图，在△ABC中，∠C=60°，AM是△ABC的角平分线，AD是△ABC的高线．
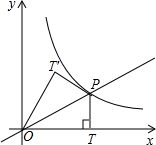如图，点P（m，1）是双曲线y=
如图，已知，AC∥BD，CP⊥EP，点E在BD上，∠ACP=60°．