题目内容
在直角坐标系中,正方形ABCD的边长为2,三点坐标A(2,0),B(2,2),C(0,2).点M是BC边上的中点,点P(0,m)是线段OC上的一个动点(C除外),直线PM交AB的延长线于点D.
(1)求点D坐标(用含m的代数式表示).
(2)若点Q是坐标平面内的一点,以APDQ为顶点的四边形是菱形,分别求出QP的坐标.
(1)求点D坐标(用含m的代数式表示).
(2)若点Q是坐标平面内的一点,以APDQ为顶点的四边形是菱形,分别求出QP的坐标.
考点:正方形的性质,坐标与图形性质,菱形的性质
专题:
分析:(1)首先根据题意画出图形画出图形,由P,M的坐标可得直线PM的方程,易求D的横坐标为2,把x=2代入即可求出其纵坐标;
(2)根据勾股定理可求出AP,DP的长,由菱形的性质可得AP=PD由此可求出Q和P的坐标.
(2)根据勾股定理可求出AP,DP的长,由菱形的性质可得AP=PD由此可求出Q和P的坐标.
解答:解:(1)设过P,M的直线为y=kx+b,把P(0,m),M(1,2)代入得:
,
解得:
.
∴PM的直线方程为y=(2-m)x+m.
将x=2代入,得y=4-m
∴D坐标为(2,4-m) ;
;
(2)由勾股定理可得AP2=m2+4,PD2=4m2-16m+20,
∵APDQ为顶点的四边形菱形,
∴AP=PD,
∴m2+4=4m2-16m+20,
解得:m=4或m=
,
又∵4-m>2,
∴m=
∴P坐标为(0.
)D坐标为(2,
)
∴Q坐标为(4,
).
|
解得:
|
∴PM的直线方程为y=(2-m)x+m.
将x=2代入,得y=4-m
∴D坐标为(2,4-m)
 ;
;(2)由勾股定理可得AP2=m2+4,PD2=4m2-16m+20,
∵APDQ为顶点的四边形菱形,
∴AP=PD,
∴m2+4=4m2-16m+20,
解得:m=4或m=
| 4 |
| 3 |
又∵4-m>2,
∴m=
| 4 |
| 3 |
∴P坐标为(0.
| 4 |
| 3 |
| 8 |
| 3 |
∴Q坐标为(4,
| 8 |
| 3 |
点评:本题考查了用待定系数法求一次函数的解析式、正方形的性质以及勾股定理的运用,题目的综合性较强,解题的关键是正确画出题目的图形.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图,在y轴上找一点C,使△ABC是等腰三角形,这样的C点共有( )个.
如图,在y轴上找一点C,使△ABC是等腰三角形,这样的C点共有( )个.| A、4 | B、3 | C、2 | D、1 |
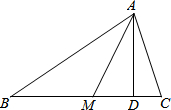 如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.
如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线. 如图,已知,AC∥BD,CP⊥EP,点E在BD上,∠ACP=60°.
如图,已知,AC∥BD,CP⊥EP,点E在BD上,∠ACP=60°. 如图,在△ABC中,AD、CE分别为BC、AB边上高,且BE:BC=1:2,∠DAC=45°,DE=3,求△ABC三边的长.
如图,在△ABC中,AD、CE分别为BC、AB边上高,且BE:BC=1:2,∠DAC=45°,DE=3,求△ABC三边的长.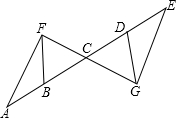 如图,CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上.求证:
如图,CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上.求证: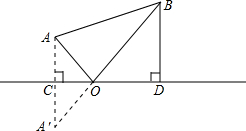 如图,A、B两个村子在河CD的同侧,AB2=13km,A、B两村子到河的距离分别为AC=1km,BD=3km.现在要在河边CD上建一水厂,向A、B村输送自来水,铺设水管的工程费为每千米3000元,请你在CD上选择水厂的位置O,使铺设水管费用的最省,并求出铺设水管的总费用W.
如图,A、B两个村子在河CD的同侧,AB2=13km,A、B两村子到河的距离分别为AC=1km,BD=3km.现在要在河边CD上建一水厂,向A、B村输送自来水,铺设水管的工程费为每千米3000元,请你在CD上选择水厂的位置O,使铺设水管费用的最省,并求出铺设水管的总费用W.