题目内容
6.计算(1)(x+2y)(x-2y)+4y(x+y)
(2)(y-1-$\frac{8}{y+1}$)÷$\frac{{y}^{2}-6y+9}{y+1}$.
分析 (1)先去括号,再合并同类项可得;
(2)先计算括号内的减法,同时将除法转化为乘法,再约分即可得.
解答 解:(1)原式=x2-4y2+4xy+4y2=x2+4xy;
(2)原式=($\frac{{y}^{2}-1}{y+1}$-$\frac{8}{y+1}$)•$\frac{y+1}{(y-3)^{2}}$
=$\frac{(y+3)(y-3)}{y+1}$•$\frac{y+1}{(y-3)^{2}}$
=$\frac{y+3}{y-3}$.
点评 本题主要考查分式的混合运算和整式的混合运算,熟练掌握混合运算的顺序和运算法则是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.由点组成的正方形,每条边上的点数n与总点数s的关系如图所示,则当n=50时,计算s的值为( )


| A. | 196 | B. | 200 | C. | 204 | D. | 198 |
17.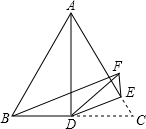 如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将
如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将
△CDE沿直线DE翻折得到△FDE,连接BF,则∠BFE的度数是( )
 如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将
如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将△CDE沿直线DE翻折得到△FDE,连接BF,则∠BFE的度数是( )
| A. | 60° | B. | 68° | C. | 75° | D. | 85° |
11.下列关于x的一元二次方程没有实数根的是( )
| A. | x2=3 | B. | x2=x | C. | x2+x+1=0 | D. | x2-x-1=0 |
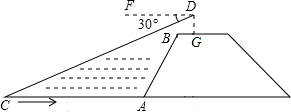 如图,小黄站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小黄的眼睛与地面的距离DG是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡AB的坡度为i=4:3,坡长AB=10.5米,则此时小船C到岸边的距离CA的长为( )米.($\sqrt{3}$≈1.7,结果保留两位有效数字)
如图,小黄站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小黄的眼睛与地面的距离DG是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡AB的坡度为i=4:3,坡长AB=10.5米,则此时小船C到岸边的距离CA的长为( )米.($\sqrt{3}$≈1.7,结果保留两位有效数字)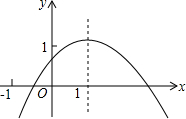 如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论: