Question

1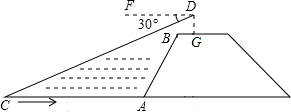．如图，小黄站在河岸上的G点，看见河里有一小船沿垂直于岸边的方向划过来．此时，测得小船C的俯角是∠FDC=30°，若小黄的眼睛与地面的距离DG是1.6米，BG=0.7米，BG平行于AC所在的直线，迎水坡AB的坡度为i=4：3，坡长AB=10.5米，则此时小船C到岸边的距离CA的长为（　　）米．（$\sqrt{3}$≈1.7，结果保留两位有效数字）

• A． 11
• B． 8.5
• C． 7.2
• D． 10

Answer 1

分析 把AB和CD都整理为直角三角形的斜边，利用坡度和勾股定理易得点B和点D到水面的距离，进而利用俯角的正切值可求得CH长度．CH-AE=EH即为AC长度．

解答 解：过点B作BE⊥AC于点E，延长DG交CA于点H，得Rt△ABE和矩形BEHG．
∵i=$\frac{BE}{AE}$=$\frac{4}{3}$，AB=10.5米，
∴BE=8.4，AE=6.3．
∵DG=1.6，BG=0.7，
∴DH=DG+GH=1.6+8.4=10，
AH=AE+EH=6.3+0.7=7．
在Rt△CDH中，
∵∠C=∠FDC=30°，DH=10，tan30°=$\frac{DH}{CH}$=$\frac{\sqrt{3}}{3}$，
∴CH=17.6．
又∵CH=CA+7，
即17.6=CA+7，
∴CA=17.6-7≈11（米）．
故选A．

点评 此题考查了俯角与坡度的知识．注意构造所给坡度和所给锐角所在的直角三角形是解决问题的难点，利用坡度和三角函数求值得到相应线段的长度是解决问题的关键．