题目内容
17.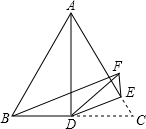 如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将
如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将△CDE沿直线DE翻折得到△FDE,连接BF,则∠BFE的度数是( )
| A. | 60° | B. | 68° | C. | 75° | D. | 85° |
分析 根据等边三角形的性质可得∠C=60°,根据等腰三角形三线合一的性质可得BD=CD,根据翻折变换的性质可得CD=DF,∠DFE=∠C,∠CDE=∠FDE,从而得到BD=DF,根据等边对等角可得∠DBF=∠DFB,然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CDF=∠DBF+∠DFB,从而求出∠DFB,再根据∠BFE=∠DFB+∠DFE计算即可得解.
解答 解:∵△ABC是等边三角形,
∴∠C=60°,
∵AD是BC边上的中线,
∴BD=CD,
∵△CDE沿直线DE翻折得到△FDE,
∴CD=DF,∠DFE=∠C=60°,∠CDE=∠FDE=25°,
∴BD=DF,
∴∠DBF=∠DFB,
由三角形的外角性质得,∠CDF=∠DBF+∠DFB=2∠DFB,
∴∠DFB=$\frac{1}{2}$∠CDF=∠CDE=25°,
∴∠BFE=∠DFB+∠DFE=25°+60°=85°.
故选D.
点评 本题考查了翻折变换的性质,等边三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,翻折前后对应边相等,对应角相等.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
7.下列语句:
①没有绝对值为-3的数;
②-a一定是一个负数;
③倒数等于它本身的数是1;
④平方数和立方数都等于它本身的数有两个,是0和1;
⑤1.249保留两个有效数字的近似值是1.3.
其中正确的有( )
①没有绝对值为-3的数;
②-a一定是一个负数;
③倒数等于它本身的数是1;
④平方数和立方数都等于它本身的数有两个,是0和1;
⑤1.249保留两个有效数字的近似值是1.3.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.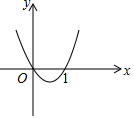 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )| A. | ①④ | B. | ②③④ | C. | ③④⑤ | D. | ①③⑤ |