题目内容
16.若一直角三角形的两边长分别为2和4,则第三边长为( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{3}$或2$\sqrt{5}$ | D. | 6 |
分析 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边4既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即4是斜边或直角边的两种情况,然后利用勾股定理求解.
解答 解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理得:
22+42=x2,
∴x=2$\sqrt{5}$;
(2)若4是斜边,则第三边x为直角边,由勾股定理得:
22+x2=42,
∴x=2$\sqrt{3}$;
∴第三边的长为2$\sqrt{3}$或2$\sqrt{5}$.
故选C.
点评 本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5.小李将1000元钱存入银行,年利率为x,第二年他把本息和全部存入银行,两年后不计利息税,他得到本息共a元,则依题意可列方程为( )
| A. | 1000(x+x)=a | B. | 1000(1-2x)=a | C. | 1000(1+x)2=a | D. | 1000(1+2x)2=a |
6.已知△ABC的三个内角∠A,∠B,∠C满足∠A=∠B=∠C,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 等边三角形 | D. | 钝角三角形 |
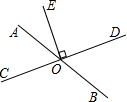 如图,已知直线AB与CD相交于点O,OE⊥CD,则∠AOE与∠DOB互余.
如图,已知直线AB与CD相交于点O,OE⊥CD,则∠AOE与∠DOB互余.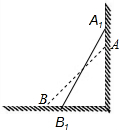 如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.
如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.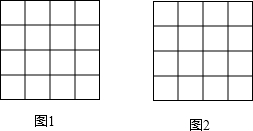 如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.