题目内容
10.有一组数:a1=$\frac{1}{2}$,a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-\frac{1}{2}}$=2,a3=$\frac{1}{1-{a}_{2}}$,…,an=$\frac{1}{1-{a}_{n-1}}$(1)a2015=2.
(2)求a1+a2+a3+…+a2015的值.
分析 (1)计算出a1、a2、a3、a4的值得出这组数每3个数为一周期,据此解答即可;
(2)由(1)知,a1+a2+a3+…+a2015中共有671个(a1+a2+a3)+a2014+a2015,列式计算可得.
解答 解:(1)∵a1=$\frac{1}{2}$,
a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-\frac{1}{2}}$=2,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-2}$=-1,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1+1}$=$\frac{1}{2}$,
∴这组数每3个数为一周期,
∵2015÷3=671…2,
∴a2015=a2=2,
故答案为:2;
(2)a1+a2+a3+…+a2015=($\frac{1}{2}$+2-1)×671+$\frac{1}{2}$+2=1009.
点评 本题主要考查数字的变化规律,根据a1、a2、a3、a4的值得出这组数每3个数为一周期是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图,AB是⊙O的直径,点C在⊙O上,D为AC上一点,BD延长线与⊙O过点A的切线相交于点E,AE=AD.
如图,AB是⊙O的直径,点C在⊙O上,D为AC上一点,BD延长线与⊙O过点A的切线相交于点E,AE=AD. 如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
 如图,长方形ABCD中,AB=8cm,AD=4cm,将△ABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点.
如图,长方形ABCD中,AB=8cm,AD=4cm,将△ABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点. 已知:如图,直线AB,CD被直线EF所截,AB∥CD,交点分别为G、H,射线GM平分∠EGB,射线HN平分∠EHD.
已知:如图,直线AB,CD被直线EF所截,AB∥CD,交点分别为G、H,射线GM平分∠EGB,射线HN平分∠EHD.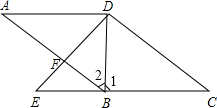 已知,如图,在四边形ABCD中,AD∥BC,点E在CB的延长线上,连接DE,交AB于点F,连接DB,且∠AFD=∠DBE,∠DBE=∠CDE.
已知,如图,在四边形ABCD中,AD∥BC,点E在CB的延长线上,连接DE,交AB于点F,连接DB,且∠AFD=∠DBE,∠DBE=∠CDE.