题目内容
2.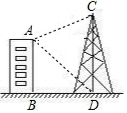 如图,已知楼房AB高50m,铁塔塔基距楼房基间的水平距离BD=50m,塔高DC为$\frac{1}{3}$(150+50$\sqrt{3}$)m,下列结论中,正确的是( )
如图,已知楼房AB高50m,铁塔塔基距楼房基间的水平距离BD=50m,塔高DC为$\frac{1}{3}$(150+50$\sqrt{3}$)m,下列结论中,正确的是( )| A. | 由楼顶望塔基俯角为60° | B. | 由楼顶望塔顶仰角为60° | ||
| C. | 由楼顶望塔基俯角为30° | D. | 由楼顶望塔顶仰角为30° |
分析 过点A作AE⊥CD于E,根据矩形的性质求出DE,得到CE的长,根据正切的概念求出∠CAE和∠EAD,判断即可.
解答 解:过点A作AE⊥CD于E,则∠EAD为楼顶望塔基俯角,∠CAE为由楼顶望塔顶仰角.
∵AB=50,
∴DE=50.
∴CE=CD=$\frac{1}{3}$(150+50$\sqrt{3}$)-50=$\frac{50\sqrt{3}}{3}$.
∴tan∠CAE=$\frac{CE}{AE}$=$\frac{\sqrt{3}}{3}$.
∴∠CAE=30°.
∵tan∠EAD=DE:AE=50:BD=1,
∴∠EAD=45°.
故选:D.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
12.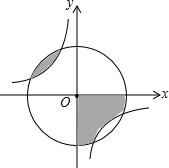 如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域的概率是( )
如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域的概率是( )
 如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域的概率是( )
如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{k}$ | D. | $\frac{1}{π}$ |
10.小强是一位密码翻译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:北、爱、我、河、游、美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
| A. | 我爱美 | B. | 河北游 | C. | 爱我河北 | D. | 美我河北 |
17.化简(1+$\frac{1}{x-2}$)÷$\frac{x-1}{{x}^{2}-4x+4}$的结果是( )
| A. | x+2 | B. | x-1 | C. | $\frac{1}{x+2}$ | D. | x-2 |
7.在一个口袋中装有4个完全相同的小球,它们的标号分别为1、2、3、4,从中随机摸出一个小球记下标号放回,再从中随机摸出一个小球,则两次摸出的小球的标号之和大于4的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{8}$ |
14.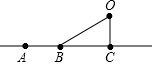 已知如图,则下列叙述不正确的是( )
已知如图,则下列叙述不正确的是( )
 已知如图,则下列叙述不正确的是( )
已知如图,则下列叙述不正确的是( )| A. | 点O不在直线AC上 | B. | 图中共有5条线段 | ||
| C. | 射线AB与射线BC是指同一条射线 | D. | 直线AB与直线CA是指同一条直线 |
 已知如图,直线AB、CD相交于点O,∠COE=90°.
已知如图,直线AB、CD相交于点O,∠COE=90°. 如图,已知四边形ABCD中∠1=∠2,AB=CD=3,BC=5,求四边形ABCD的周长.
如图,已知四边形ABCD中∠1=∠2,AB=CD=3,BC=5,求四边形ABCD的周长.