题目内容
11. 已知如图,直线AB、CD相交于点O,∠COE=90°.
已知如图,直线AB、CD相交于点O,∠COE=90°.(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
分析 (1)根据平角的定义求解即可;
(2)根据平角的定义可求∠BOD,根据对顶角的定义可求∠AOC,根据角的和差关系可求∠AOE的度数;
(3)先过点O作OF⊥AB,再分两种情况根据角的和差关系可求∠EOF的度数.
解答  解:(1)∵∠AOC=36°,∠COE=90°,
解:(1)∵∠AOC=36°,∠COE=90°,
∴∠BOE=180°-∠AOC-∠COE=54°;
(2)∵∠BOD:∠BOC=1:5,
∴∠BOD=180°×$\frac{1}{1+5}$=30°,
∴∠AOC=30°,
∴∠AOE=30°+90°=120°;
(3)如图1,∠EOF=120°-90°=30°,
或如图2,∠EOF=360°-120°-90°=150°.
故∠EOF的度数是30°或150°.
点评 本题主要考查了角的计算,涉及到的角有平角、直角;熟练掌握平角等于180度,直角等于90度,是解答本题的关键.

练习册系列答案
相关题目
1.下面合并同类项正确的是( )
| A. | 3x+2x2=5x3 | B. | 2a2b-2a2b-a2b=1 | C. | -ab-ab=0 | D. | -xy2+xy2=0 |
2.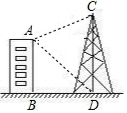 如图,已知楼房AB高50m,铁塔塔基距楼房基间的水平距离BD=50m,塔高DC为$\frac{1}{3}$(150+50$\sqrt{3}$)m,下列结论中,正确的是( )
如图,已知楼房AB高50m,铁塔塔基距楼房基间的水平距离BD=50m,塔高DC为$\frac{1}{3}$(150+50$\sqrt{3}$)m,下列结论中,正确的是( )
 如图,已知楼房AB高50m,铁塔塔基距楼房基间的水平距离BD=50m,塔高DC为$\frac{1}{3}$(150+50$\sqrt{3}$)m,下列结论中,正确的是( )
如图,已知楼房AB高50m,铁塔塔基距楼房基间的水平距离BD=50m,塔高DC为$\frac{1}{3}$(150+50$\sqrt{3}$)m,下列结论中,正确的是( )| A. | 由楼顶望塔基俯角为60° | B. | 由楼顶望塔顶仰角为60° | ||
| C. | 由楼顶望塔基俯角为30° | D. | 由楼顶望塔顶仰角为30° |
19.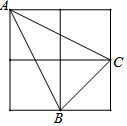 如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形的个数有(不包含△ABC本身)( )
如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形的个数有(不包含△ABC本身)( )
 如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形的个数有(不包含△ABC本身)( )
如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形的个数有(不包含△ABC本身)( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16. 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )
 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 三棱柱 | D. | 三棱锥 |
19.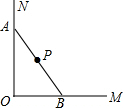 如图,一根长为a的木棍(AB),斜靠在与地面(OM)垂直的墙上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑动,在滑动的过程中OP的长度( )
如图,一根长为a的木棍(AB),斜靠在与地面(OM)垂直的墙上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑动,在滑动的过程中OP的长度( )
 如图,一根长为a的木棍(AB),斜靠在与地面(OM)垂直的墙上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑动,在滑动的过程中OP的长度( )
如图,一根长为a的木棍(AB),斜靠在与地面(OM)垂直的墙上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑动,在滑动的过程中OP的长度( )| A. | 减小 | B. | 增大 | C. | 不变 | D. | 先减小再增大 |
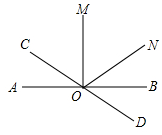 如图,直线AB与CD相交于点O,∠AOM=90°,且OM平分∠NOC.若∠BOC=4∠NOB,求∠MON的度数.
如图,直线AB与CD相交于点O,∠AOM=90°,且OM平分∠NOC.若∠BOC=4∠NOB,求∠MON的度数.