题目内容
5.对于实数x,我们规定[x)表示大于x的最小整数,如[4)=5,[$\sqrt{3}$)=2,[-2.5)=-2,现对64进行如下操作:64$\stackrel{第1次}{→}$[$\sqrt{64}$)=9$\stackrel{第2次}{→}$[$\sqrt{9}$)=4$\stackrel{第3次}{→}$[$\sqrt{4}$)=3$\stackrel{第4次}{→}$[$\sqrt{3}$)=2,这样对64只需进行4次操作后变为2,类似地,只需进行4次操作后变为2的所有正整数中,最大的是3968.分析 将63代入操作程序,只需要3次后变为2,设这个最大正整数为m,则$\sqrt{m}<63$,从而求得这个最大的数.
解答 解:63$\stackrel{第1次}{→}$[$\sqrt{63}$)=8$\stackrel{第2次}{→}$[$\sqrt{8}$)=3$\stackrel{第3次}{→}$[$\sqrt{3}$)=2,
设这个最大正整数为m,则m$\stackrel{第1次}{→}$[$\sqrt{m}$)=63,
∴$\sqrt{m}$<63.
∴m<3969.
∴m的最大正整数值为3968.
点评 本题主要考查的是新定义,确定出经过3次变化后值为2的最大正整数值是解题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
15.某种商品经连续两次降价后价格为原来的81%,设价格平均每次下降百分率为x,则可列方程( )
| A. | (1-x)2=81% | B. | (1+x)2=81% | C. | 1-2x=81% | D. | 1+2x=81% |
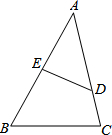 如图,在△ABC中,点D、E分别在边AC、AB上,且$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,若DE=4,则BC=6.
如图,在△ABC中,点D、E分别在边AC、AB上,且$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,若DE=4,则BC=6.