题目内容
20.已知|x-12|+|z-13|+y2-10y+25=0,则以x、y、z为三边的三角形是直角三角形.分析 先根据非负数的性质求出x、y、z的值,再根据勾股定理的逆定理进行解答即可.
解答 解:以x,y,z为三边的三角形是直角三角形.
∵|x-12|+|z-13|+y2-10y+25=0,
∴|x-12|+|z-13|+(y-5)2=0,
∴x-12=0,z-13=0,y-5=0,
∴x=12,y=5,z=13,
∵122+52=132,
∴以x,y,z为三边的三角形是直角三角形.
故答案为直角.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
10.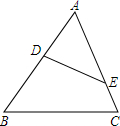 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )| A. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
11.下列哪个方程是一元二次方程( )
| A. | x+2y=1 | B. | 2x(x-1)-2x+3=0 | C. | $\frac{1}{{x}^{2}}$+4x=3 | D. | x2-2xy=0 |
9.一副扑克牌54张牌,从中任抽一张牌,抽到大王或小王的概率为( )
| A. | $\frac{1}{54}$ | B. | $\frac{1}{27}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{3}$ |
10.下列说法正确的是( )
| A. | 带根号的数都是无理数 | B. | 无理数一定是无限不循环小数 | ||
| C. | 无理数与无理数的和是无理数 | D. | 有理数与无理数的积是无理数 |