题目内容
15.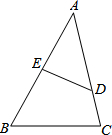 如图,在△ABC中,点D、E分别在边AC、AB上,且$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,若DE=4,则BC=6.
如图,在△ABC中,点D、E分别在边AC、AB上,且$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,若DE=4,则BC=6.
分析 先证明△ADE∽△ABC,得出对应边的比等于相似比,即可得出结果.
解答 解:∵$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,∠A=∠A,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AE}{AC}=\frac{2}{3}$,
即$\frac{4}{BC}=\frac{2}{3}$,
解得:BC=6;
故答案为:6.
点评 本题考查了相似三角形的判定与性质;熟记两边成比例且夹角相等的两个三角形相似是解决问题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
10.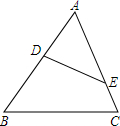 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
 如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )
如图,在△ABC中,∠ADE=∠C,那么下列等式中,成立的是( )| A. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
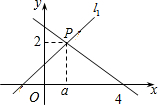 如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(a,2).
如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(a,2). 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.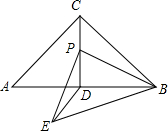 等腰直角三角形ABC的斜边AB的长为4,CD为边AB上的高线,P为CD上的一点,以BP为直角边向下作等腰直角三角形BPE,如图所示,则DE的最小值为$\sqrt{2}$.
等腰直角三角形ABC的斜边AB的长为4,CD为边AB上的高线,P为CD上的一点,以BP为直角边向下作等腰直角三角形BPE,如图所示,则DE的最小值为$\sqrt{2}$.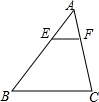 如图,△ABC中,点E在边AB上,过点E作EF∥BC交AC于点F,若$\frac{AE}{EB}$=$\frac{1}{2}$,S△AEF=1,则四边形EBCF的面积为( )
如图,△ABC中,点E在边AB上,过点E作EF∥BC交AC于点F,若$\frac{AE}{EB}$=$\frac{1}{2}$,S△AEF=1,则四边形EBCF的面积为( )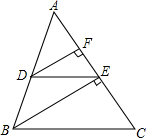 如图,在△ABC中,DE∥BC,BE⊥AC于点E,DF⊥AC于点F,若DE=2,BC=4,BE=2$\sqrt{3}$,且△ABC的周长为12,求△ADE的周长和DF的长度.
如图,在△ABC中,DE∥BC,BE⊥AC于点E,DF⊥AC于点F,若DE=2,BC=4,BE=2$\sqrt{3}$,且△ABC的周长为12,求△ADE的周长和DF的长度. 如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其沿CD折叠,使点A落在边CB上的点A′处,则∠A′DB度数是10°.
如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其沿CD折叠,使点A落在边CB上的点A′处,则∠A′DB度数是10°.