题目内容
11．若k=$\frac{a-2b}{c}$=$\frac{b-2c}{a}$=$\frac{c-2a}{b}$，且a+b+c≠0，求k的值．分析 根据比例的性质，即可解答．
解答 解：∵k=$\frac{a-2b}{c}$=$\frac{b-2c}{a}$=$\frac{c-2a}{b}$，且a+b+c≠0，
∴k=$\frac{a-2b+b-2c+c-2a}{a+b+c}=\frac{-a-b-c}{a+b+c}$=$\frac{-（a+b+c）}{a+b+c}$=-1．
点评 本题考查了比例的性质，解决本题的关键是熟记比例的性质．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
1．在一次体育测试中，小芳所在小组8人的成绩分别是66，67，78，78，79，79，79，80，则这8人体育成绩的中位数是（ ）
| A． | 77 | B． | 78 | C． | 78.5 | D． | 79 |
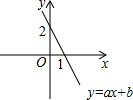函数y=ax+b的图象如图所示，则不等式组$\left\{\begin{array}{l}{ax+b＞0}\\{x+2＞0}\end{array}\right.$的解集为-2＜x＜1．
如图，∠AOB=90°，OD平分∠BOC，∠DOE=45°，则∠AOE=∠COE（填“＜”“＞”或“=”号）
如图，在∠AOB内找一点P，使得点P到∠AOB的两边距离相等，且使点P到点C的距离最短（尺规作图，请保留作图痕迹）．