题目内容
19．已知x=1是不等式组$\left\{\begin{array}{l}{3（x-1）＞x+2a}\\{\frac{3x-5}{2}≤x-2a}\end{array}\right.$的一个解，求a的取值范围．分析 把x=1代入不等式组，再求出不等式组的解集即可．
解答 解：把x=1代入不等式组$\left\{\begin{array}{l}{3（x-1）＞x+2a}\\{\frac{3x-5}{2}≤x-2a}\end{array}\right.$得：$\left\{\begin{array}{l}{0＞1+2a①}\\{-1≤1-2a②}\end{array}\right.$，
解不等式①得：a＜-$\frac{1}{2}$，
解不等式②得：a≤1，
所以a的取值范围是-$\frac{1}{2}$＜a≤1．
点评 本题考查了解一元一次不等式组和一元一次不等式组的解的应用，解此题的关键是得出关于a的不等式组．
练习册系列答案
相关题目
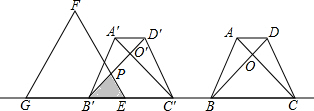
如图，已知等边△ABC，以AB为直径的半圆与BC边交于点D，过点D作⊙O的切线DF交AC于点F，过点D作DE⊥AB，垂足为点E，过点F作FG⊥AB，垂足为点G，连结GD．
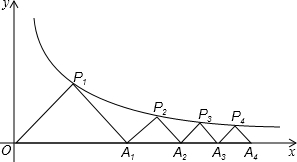如图，△P1OA1，△P2A1A2，△P2A2A3…，是等腰直角三角形，点P1，P2，P3…在反比例函数y=$\frac{4}{x}$的图象上，斜边OA1，A1A2，A2A3…都在x轴上，则点A2的坐标是（4$\sqrt{2}$，0），A3的坐标是（4$\sqrt{3}$，0），An的坐标是（4$\sqrt{n}$，0）．
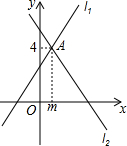如图，直线l1：y=x+3与直线l2：y=ax+b相交于点A（m，4）．
如图，正方形ABCD的边长为a，分别以A、B为圆心，a为半径在正方形内作弧，求图中阴影部分的面积．