题目内容
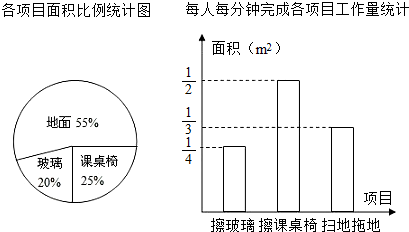
13.一次函数y=kx+b(k≠0)的图象经过点B(2,0),C(0,6)两点,则kx+b≥2x的解集是( )| A. | x≤$\frac{6}{5}$ | B. | x<2 | C. | x$<\frac{6}{5}$ | D. | x≤2 |
分析 先利用一次函数解析式确定A点坐标,然后观察函数图象得到,当x>1时,直线y=2x都在直线y=kx+b的上方,当x<2时,直线y=kx+b在x轴上方,于是可得到不等式kx+b≥2x的解集.
解答 解:因为一次函数y=kx+b(k≠0)的图象经过点B(2,0),C(0,6)两点,
可得:$\left\{\begin{array}{l}{b=6}\\{2k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=6}\end{array}\right.$,
所以解析式为:y=-3x+6;
联立两个方程可得:$\left\{\begin{array}{l}{y=2x}\\{y=-3x+6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{6}{5}}\\{y=\frac{12}{5}}\end{array}\right.$,
所以kx+b≥2x的解集是$x≤\frac{6}{5}$;
故选A
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,用10块相同的长方形的地砖拼成一个长方形,则每块长方形地砖的面积为( )
如图,用10块相同的长方形的地砖拼成一个长方形,则每块长方形地砖的面积为( )
 如图,用10块相同的长方形的地砖拼成一个长方形,则每块长方形地砖的面积为( )
如图,用10块相同的长方形的地砖拼成一个长方形,则每块长方形地砖的面积为( )| A. | 128 | B. | 256 | C. | 512 | D. | 1024 |
2.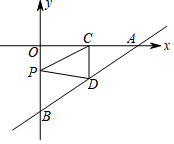 如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
 如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )| A. | (0,-1) | B. | (0,-2) | C. | (0,-3) | D. | (0,-4) |
 学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).
学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹). 如图,△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC于D,AB=15,BD=9,CD=5,则⊙O的半径为$\frac{65}{8}$.
如图,△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC于D,AB=15,BD=9,CD=5,则⊙O的半径为$\frac{65}{8}$.