题目内容
9. 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
分析 延长EC交圆于点F,连接DF.则根据90°的圆周角所对的弦是直径,得DF是直径.根据射影定理先求直径,再得半径.
解答 解:延长EC交圆于点F,连接DF,
则根据90°的圆周角所对的弦是直径,得DF是直径,
∵DE∥BC,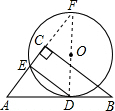
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AE}{AC}$,
∴DE=4,
在直角△ADF中,根据射影定理,得
EF=$\frac{{DE}^{2}}{AE}$=4$\sqrt{2}$,
根据勾股定理,得DF=$\sqrt{{EF}^{2}{+DE}^{2}}$=4$\sqrt{3}$,
则圆的半径是2$\sqrt{3}$.
故选C.
点评 此题主要考查了切线的性质,能够通过作辅助线,把直径构造到直角三角形中,熟练运用相似三角形的性质、圆周角定理的推论以及射影定理和勾股定理是解答此题的关键.

练习册系列答案
相关题目
20.速录员小明打2500个字和小刚打3000个字所用的时间相同,已知小刚每分钟比小明多打50个字,求两人的打字速度.设小刚每分钟打x个字,根据题意列方程,正确的是( )
| A. | $\frac{2500}{x}$=$\frac{3000}{x-50}$ | B. | $\frac{2500}{x}$=$\frac{3000}{x+50}$ | C. | $\frac{2500}{x-50}$=$\frac{3000}{x}$ | D. | $\frac{2500}{x+50}$=$\frac{3000}{x}$ |
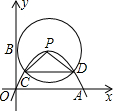 如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).
如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).