题目内容
18.如果$\frac{2}{3}$a2xb2y与3a3ybx+1是同类项,那么$\root{3}{y-x}$的值为( )| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
分析 根据同类项的定义可知所含字母相同,相同字母的指数也相同,从而可以得到x、y的关系式,从而可以得到x、y的值,从而可以求出$\root{3}{y-x}$的值.
解答 解:∵$\frac{2}{3}$a2xb2y与3a3ybx+1是同类项,
∴$\left\{\begin{array}{l}{2x=3y}\\{2y=x+1}\end{array}\right.$
解得,$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$
∴$\root{3}{y-x}$=$\root{3}{2-3}=\root{3}{-1}=-1$,
故选D.
点评 本题考查立方根、同类项、解二元一次方程组,解题的关键是明确立方根的求法、同类项的定义、解二元一次方程组的解法,注意同类项一定要找好对应的量.

练习册系列答案
相关题目
13. 如图,在△ABC中,∠B=60°,∠C=40°,EF∥AB,则∠1的度数为( )
如图,在△ABC中,∠B=60°,∠C=40°,EF∥AB,则∠1的度数为( )
 如图,在△ABC中,∠B=60°,∠C=40°,EF∥AB,则∠1的度数为( )
如图,在△ABC中,∠B=60°,∠C=40°,EF∥AB,则∠1的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
7.下列各数:3.14159,$\root{3}{64}$,π,$\frac{22}{7}$,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.如果反比例函数y=$\frac{k}{x}$的图象经过点(-2,3),那么该函数的图象也经过点( )
| A. | (-2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
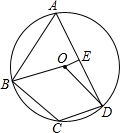 如图,点A,B,C,D在⊙O上,∠ABO=40°,∠BCD=112°,E是AD中点,则∠DOE的度数为62°.
如图,点A,B,C,D在⊙O上,∠ABO=40°,∠BCD=112°,E是AD中点,则∠DOE的度数为62°.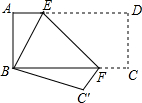 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB=55度.
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB=55度.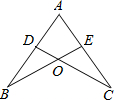 如图,已知点D在AB上,点E在AC上,AB=AC,请你再补充一个条件,使△ABE≌△ACD.你补充的条件是∠B=∠C或AD=AE.
如图,已知点D在AB上,点E在AC上,AB=AC,请你再补充一个条件,使△ABE≌△ACD.你补充的条件是∠B=∠C或AD=AE.