题目内容
6.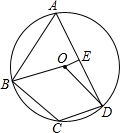 如图,点A,B,C,D在⊙O上,∠ABO=40°,∠BCD=112°,E是AD中点,则∠DOE的度数为62°.
如图,点A,B,C,D在⊙O上,∠ABO=40°,∠BCD=112°,E是AD中点,则∠DOE的度数为62°.
分析 首先连接OA,由等腰三角形的性质与圆的内接四边形的性质,求得∠BAO与∠BAD的度数,则可求得∠DAO的度数,又由垂径定理,即可求得答案.
解答  解:连接OA,
解:连接OA,
∵OA=OB,∠ABO=40°,
∴∠OAB=∠ABO=40°,
∵∠BCD=112°,
∴∠BAD=180°-∠BCD=68°,
∴∠OAE=∠BAD-∠OAB=28°,
∵OA=OD,
∴∠ODA=∠OAD=28°
∵E是AD中点,
∴OE⊥AD,
∴∠DOE=90°-∠ODA=62°.
故答案为:62°.
点评 此题考查了圆周角定理、垂径定理、圆的内接四边形的性质以及等腰三角形的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
16.下列:①${({-\frac{1}{5}})^{-2}}=25$;②(-2016)0=1;③(a-b)2=a2-b2;④(-2ab3)3=-8a3b9;⑤5x2-6x=-x.其中计算正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ③④⑤ | D. | ②④⑤ |
11.某市努力改善空气质量,近年来空气质量明显好转,根据该市环境保护局公布的2010-2014这五年各年全年空气质量优良的天数如表所示,根据表中信息回答:
(1)这五年的全年空气质量优良天数的中位数是245,平均数是243;
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是2012年(填写年份);
(3)求这五年的全年空气质量优良天数的方差.
| 2010 | 2011 | 2012 | 2013 | 2014 |
| 234 | 233 | 245 | 247 | 256 |
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是2012年(填写年份);
(3)求这五年的全年空气质量优良天数的方差.




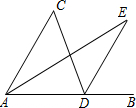 如图,点B是AD延长线上的一点,DE∥AC,AE平分∠CAB,∠C=50°,∠E=30°,则∠CDA的度数等于70°.
如图,点B是AD延长线上的一点,DE∥AC,AE平分∠CAB,∠C=50°,∠E=30°,则∠CDA的度数等于70°.
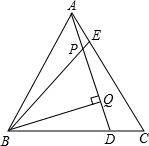 如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.
如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.