题目内容
9.已知关于x的分式方程$\frac{x}{x-2}$=$\frac{a}{x-2}$+2无解,求关于y的不等式$\frac{ay-1}{3}$-$\frac{9y+a}{6}$≤1的解集,并在数轴上把解集表示出来.分析 先把分式方程化为整式方程,解得x=4-a,利用分式方程无解可得到a=2,则不等式化为$\frac{2y-1}{3}$-$\frac{9y+2}{6}$≤1,然后解不等式得到y≥-2,最后用数轴表示解集.
解答 解:去分母得到x=a+2(x-2),
解得x=4-a,
因为分式方程无解,则x=2,
所以4-a=2,解得a=2,
不等式化为$\frac{2y-1}{3}$-$\frac{9y+2}{6}$≤1,
2(2y-1)-(9y+2)≤6,
4y-2-9y-2≤6,
-5y≤10,
所以y≥-2,
用数轴表示为:
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
19.若线段CD是由线段AB平移得到的,点A(-1,3)的对应点为C(2,2),则点B(-3,-1)的对应点D的坐标是( )
| A. | (0,-2) | B. | (1,-2) | C. | (-2,0) | D. | (4,6) |
4. 如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )
如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )
 如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )
如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )| A. | BC的垂直平分线与AC的垂直平分线的交点 | |
| B. | ∠C的平分线与BC的垂直平分线的交点 | |
| C. | ∠C的平分线与AC的垂直平分线的交点 | |
| D. | ∠C的平分线与AB的垂直平分线的交点 |




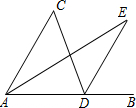 如图,点B是AD延长线上的一点,DE∥AC,AE平分∠CAB,∠C=50°,∠E=30°,则∠CDA的度数等于70°.
如图,点B是AD延长线上的一点,DE∥AC,AE平分∠CAB,∠C=50°,∠E=30°,则∠CDA的度数等于70°.
 我市某风景区门票价格如图所示,百姓旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,百姓旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.