题目内容
17.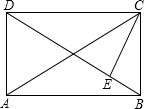 已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE.
已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE.
分析 由矩形的性质得出∠BCD=90°,OB=OC,得出∠OCB=∠OBC,求出∠ECB,得出∠OBC、OCB、∠OCE,证出△OCE是等腰直角三角形,即可得出CE=OE.
解答 证明:如图所示: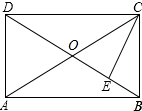 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠BCD=90°,OC=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OB=OC,
∴∠OCB=∠OBC,
∵∠DCE:∠ECB=3:1,
∴∠ECB=$\frac{1}{4}$×90°=22.5°,
∵CE⊥BD,
∴∠BEC=90°,
∴∠OBC=90°-22.5°=67.5°,
∴∠OCB=67.5°,
∴∠OCE=45°,
∴△OCE是等腰直角三角形,
∴CE=OE.
点评 本题考查了矩形的性质、等腰三角形的性质、等腰直角三角形的判定与性质;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
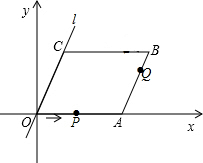 如图,在平面直角坐标系中,四边形OABC是平行四边形,直线l经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C-B相交于点M.当M、Q两点相遇时停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.
如图,在平面直角坐标系中,四边形OABC是平行四边形,直线l经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C-B相交于点M.当M、Q两点相遇时停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.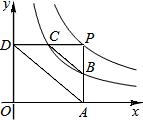 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上任意一点,PA⊥x轴于A,PD⊥y轴于点D,分别交反比例函数y=$\frac{k}{x}$(x>0,0<k<6)的图象于点B,C.下列结论:
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上任意一点,PA⊥x轴于A,PD⊥y轴于点D,分别交反比例函数y=$\frac{k}{x}$(x>0,0<k<6)的图象于点B,C.下列结论: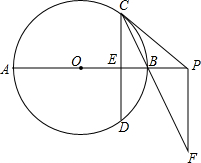 如图,已知AB是⊙O的直径,弦CD⊥AB于E,过C点的切线交AB的延长线于P,过P点作PF∥CD交CB的延长线于F.
如图,已知AB是⊙O的直径,弦CD⊥AB于E,过C点的切线交AB的延长线于P,过P点作PF∥CD交CB的延长线于F.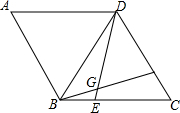 在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.
在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.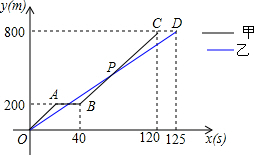 在运动会径赛中,甲、乙同时起跑,刚跑出200m,甲不慎摔倒,他又迅速地爬起来继续投入比赛,若他们所跑的路程y(m)与比赛时间x(s)的关系如图,有下列说法:①他们进行的是800m比赛;②乙全程的平均速度为6.4m/s;③甲摔倒之前,乙的速度快;④甲再次投入比赛后的平均速度为7.5m/s;⑤甲再次投入比赛后在距离终点300米时追上了乙.其中正确的个数有( )
在运动会径赛中,甲、乙同时起跑,刚跑出200m,甲不慎摔倒,他又迅速地爬起来继续投入比赛,若他们所跑的路程y(m)与比赛时间x(s)的关系如图,有下列说法:①他们进行的是800m比赛;②乙全程的平均速度为6.4m/s;③甲摔倒之前,乙的速度快;④甲再次投入比赛后的平均速度为7.5m/s;⑤甲再次投入比赛后在距离终点300米时追上了乙.其中正确的个数有( ) △ABC中,点D在边AC上,AB=AC,AD=BD=BC,求出∠A的度数.
△ABC中,点D在边AC上,AB=AC,AD=BD=BC,求出∠A的度数.