题目内容
7.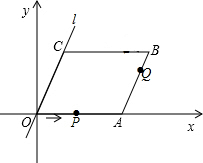 如图,在平面直角坐标系中,四边形OABC是平行四边形,直线l经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C-B相交于点M.当M、Q两点相遇时停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.
如图,在平面直角坐标系中,四边形OABC是平行四边形,直线l经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C-B相交于点M.当M、Q两点相遇时停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.(1)点C的坐标为(3,4),直线l的解析式为y=$\frac{4}{3}$x;
(2)若抛物线C′经过O、A、C三点,则抛物线C′的开口方向:向下,对称轴方程:x=4;
(3)试求点Q与点M相遇前S与t的函数关系式,并求出S的最大值.
分析 (1)根据点A和点B的坐标,写出点C的坐标,然后求出直线l的函数解析式;
(2)根据点A、O、C的位置可得抛物线C′的开口方向向下,对称轴为x=4;
(3)根据题意,得OP=t,AQ=2t.分三种情况讨论:①当0<t≤$\frac{5}{2}$时;②当$\frac{5}{2}$<t≤3时;③当3<t<$\frac{16}{3}$时,分别表示出MP、PE的长度,然后根据S=$\frac{1}{2}$•MP•PE,求出S与t的函数关系式,然后根据配方法求出S的最大值.
解答 解:(1)∵点A的坐标为(8,0),点B的坐标为(11,4),四边形OABC是平行四边形,
∴点C的坐标是(3,4),
∴直线l的解析式为:y=$\frac{4}{3}$x;
(2)∵抛物线C′经过O、A、C三点,
∴抛物线C′的开口向下,
对称轴为:x=4;
(3)根据题意,得OP=t,AQ=2t.分三种情况讨论: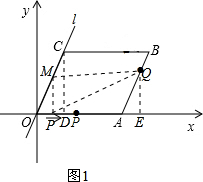
①当0<t≤$\frac{5}{2}$时,如图1,M点的坐标是(t,$\frac{4}{3}$t).
过点C作CD⊥x轴于D,过点Q作QE⊥x轴于E,可得△AEQ∽△ODC.
∴$\frac{AQ}{OC}$=$\frac{AE}{OD}$=$\frac{QE}{CD}$,
∴$\frac{2t}{5}$=$\frac{AE}{3}$=$\frac{QE}{4}$,
∴AE=$\frac{6t}{5}$,EQ=$\frac{8}{5}$t.
∴Q点的坐标是(8+$\frac{6t}{5}$,$\frac{8}{5}$t),
∴PE=8+$\frac{6t}{5}$-t=8+$\frac{1}{5}$t.
∴S=$\frac{1}{2}$•MP•PE=$\frac{1}{2}$•$\frac{4}{3}$t•(8+$\frac{1}{5}$t)=$\frac{2}{15}$t2+$\frac{16}{3}$t=$\frac{2}{15}$(t+20)2-$\frac{160}{3}$,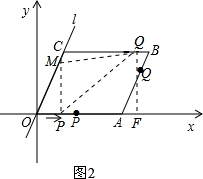
∵当0<t≤$\frac{5}{2}$时,S随t的增大而增大,
∴当t=$\frac{5}{2}$时,S有最大值,最大值为$\frac{85}{6}$.
②当$\frac{5}{2}$<t≤3时,如图2,过点Q作QF⊥x轴于F,
∵BQ=2t-5,
∴OF=11-(2t-5)=16-2t,
∴Q点的坐标是(16-2t,4),
∴PF=16-2t-t=16-3t.
∴S=$\frac{1}{2}$•MP•PE=$\frac{1}{2}$•$\frac{4}{3}$t•(16-3t)=-2t2+$\frac{32}{3}$t=-2(t-$\frac{8}{3}$)2+$\frac{128}{9}$,
∴当t=$\frac{8}{3}$时,S有最大值,最大值为$\frac{128}{9}$,
③当3<t<$\frac{16}{3}$时,如图3,
∴MQ=16-2t-t=16-3t,MP=4.
∴S=$\frac{1}{2}$•MP•PE=$\frac{1}{2}$•4•(16-3t)=-6t+32.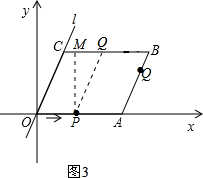
∵k=-6<0.
∴S随t的增大而减小.
又∵当t=3时,S=14.当t=$\frac{16}{3}$时,S=0.
∴0<S<14.
综上所述,S与t函数关系式为S=$\left\{\begin{array}{l}{\frac{2}{15}{t}^{2}+\frac{16}{3}t(0<t≤\frac{5}{2})}\\{-2{t}^{2}+\frac{32}{3}t(\frac{5}{2}<t≤3)}\\{-6t+32(3<t<\frac{16}{3})}\end{array}\right.$,
当t=$\frac{8}{3}$时,S有最大值,最大值为$\frac{128}{9}$.
点评 本题是二次函数的综合题,其中涉及到的知识点有抛物线最大值的求法和动点问题等知识点,是各地中考的热点和难点,解题时注意数形结合和分类讨论等数学思想的运用,同学们要加强训练,此题难度较大.

 如图,直线a∥b,c⊥d,∠1=44°,那∠2的度数为( )
如图,直线a∥b,c⊥d,∠1=44°,那∠2的度数为( )| A. | 46° | B. | 44° | C. | 36° | D. | 22° |
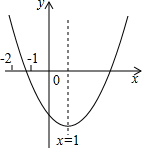 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②b+2a=0;③8a+c>0;④a+3b+c>0.
其中,正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | (2x-4y)2 | B. | (2x-4y)(2x+4y) | C. | 4(x2-4y2) | D. | 4(x-2y)(x+2y) |

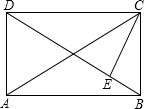 已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE.
已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE.