题目内容
9.(1)化简:$\frac{{{a^2}-1}}{{{a^2}+6a+9}}÷(a+1)×\frac{{{a^2}-9}}{a-1}$(2)化简计算:$\frac{a-1}{{{a^2}-4a+4}}×\frac{{{a^2}-4}}{2a-2}$,其中a=-1.
分析 (1)根据分式化简的方法,把$\frac{{{a^2}-1}}{{{a^2}+6a+9}}÷(a+1)×\frac{{{a^2}-9}}{a-1}$化简即可.
(2)首先根据分式化简的方法,把分式$\frac{a-1}{{{a^2}-4a+4}}×\frac{{{a^2}-4}}{2a-2}$进行化简,然后把a=-1代入化简后的算式,求出算式的值是多少即可.
解答 解:(1)$\frac{{{a^2}-1}}{{{a^2}+6a+9}}÷(a+1)×\frac{{{a^2}-9}}{a-1}$
=$\frac{(a+1)(a-1)}{{(a+3)}^{2}}$•$\frac{1}{a+1}$•$\frac{(a+3)(a-3)}{a-1}$
=$\frac{a-3}{a+3}$;
(2)$\frac{a-1}{{{a^2}-4a+4}}×\frac{{{a^2}-4}}{2a-2}$
=$\frac{a-1}{{(a-2)}^{2}}$×$\frac{(a-2)(a+2)}{2(a-1)}$
=$\frac{a+2}{2(a-2)}$
则当a=-1时,原式=$\frac{a+2}{2(a-2)}$=$\frac{-1+2}{2×(-1-2)}$=-$\frac{1}{6}$.
点评 (1)此题主要考查了分式的化简求值问题,要熟练掌握,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.
(2)此题还考查了分式的混合运算,要熟练掌握,解答此题的关键是要明确:分式的混合运算,先乘方,再乘除,然后加减,有括号的先算括号里面的.

练习册系列答案
相关题目
4.十二边形的外角和是( )
| A. | 1080° | B. | 1800° | C. | 720° | D. | 360° |
1.学校组织了一次知识竞赛,共有25道题,每一道题答对得5分,答错或不答都扣3分,小明得了85分,那么他答对的题数是( )
| A. | 22 | B. | 20 | C. | 19 | D. | 18 |
18.如果二元一次方程组$\left\{\begin{array}{l}{x+y=2a}\\{x-y=4a}\end{array}\right.$的解是方程2x+3y-3=0的一个解,那么a的值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
19.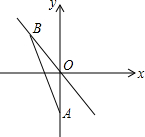 如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )
如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )
 如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )
如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | (1,-1) | C. | ($\frac{1}{2}$,-$\frac{1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
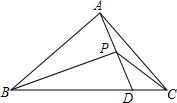 如图,在△ABC中(AB<BC),在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为3,则△BPC的面积为$\frac{3}{2}$.
如图,在△ABC中(AB<BC),在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为3,则△BPC的面积为$\frac{3}{2}$.