题目内容
19.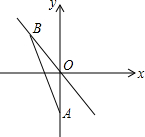 如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )
如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | (1,-1) | C. | ($\frac{1}{2}$,-$\frac{1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
分析 根据A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,可知当AB⊥OB时,线段AB最短,作辅助线BC⊥OA于点C,可得OC=CB,由点A(0,-$\sqrt{2}$),可得点B的坐标,从而本题得以解决.
解答 解:∵A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,
∴当AB⊥OB时,线段AB最短,此时点B在第四象限,作BC⊥OA于点C,∠AOB=45°,如下图所示: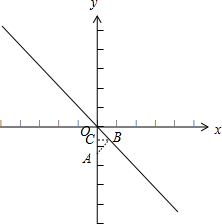
∴OC=CB=$\frac{1}{2}$OA,
∴点B的坐标为($\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}$)
故选D.
点评 本题考查一次函数图象上点的坐标特征和垂线段最短,解题的关键是明确直线外一点到直线的所有线段中垂线段最短,直线y=-x与两坐标轴的夹角为45°.

练习册系列答案
相关题目
14.某广告公司欲招聘广告策划人员一名,对A,B两名候选人进行了三项素质测试,他们的各项测试成绩如表所示:根据实际需要,公司将创新、综合和语言三项测试得分按4:3:1的比例确定两人的测试成绩,此时谁将被录用?
| 测试项目 | 测试成绩/分 | |
| A | B | |
| 创新 | 85 | 70 |
| 综合知识 | 50 | 80 |
| 语言 | 88 | 75 |
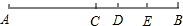 如图,C是AB中点,D是BC上一点,E是BD的中点,AB=20,CD=2,求EB,CE的长.
如图,C是AB中点,D是BC上一点,E是BD的中点,AB=20,CD=2,求EB,CE的长.
 如图,已知P、M、N三点,按下面要求画出图形;
如图,已知P、M、N三点,按下面要求画出图形;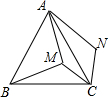 如图,M为等边△ABC内部的一点,且MA=8,MB=10,MC=6,将△BMC绕点C顺时针旋转得到△ANC.下列说法中:①MC=NC;②AM=AN;③S四边形AMCN=S△ABC-S△ABM;④∠AMC=120°.正确的有①③.(请填上番号)
如图,M为等边△ABC内部的一点,且MA=8,MB=10,MC=6,将△BMC绕点C顺时针旋转得到△ANC.下列说法中:①MC=NC;②AM=AN;③S四边形AMCN=S△ABC-S△ABM;④∠AMC=120°.正确的有①③.(请填上番号)