Question

17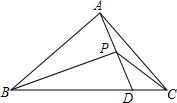．如图，在△ABC中（AB＜BC），在BC上截取BD=BA，作∠ABC的平分线与AD相交于点P，连接PC，若△ABC的面积为3，则△BPC的面积为$\frac{3}{2}$．

Answer 1

分析 根据等腰三角形三线合一的性质可得AP=PD，然后根据等底等高的三角形面积相等求出△BPC的面积等于△ABC面积的一半，代入数据计算即可得解．

解答 解：∵BD=BA，BP是∠ABC的平分线，
∴AP=PD，
∴S_△BPD=$\frac{1}{2}$S_△ABD，S_△CPD=$\frac{1}{2}$S_△ACD，
∴S_△BPC=S_△BPD+S_△CPD=$\frac{1}{2}$S_△ABD+$\frac{1}{2}$S_△ACD=$\frac{1}{2}$S_△ABC，
∵△ABC的面积为3，
∴S_△BPC=$\frac{1}{2}$×3=$\frac{3}{2}$．
故答案为：$\frac{3}{2}$．

点评 本题考查了等腰三角形三线合一的性质，三角形的面积，利用等底等高的三角形的面积相等求出△BPC的面积与△ABC的面积的关系是解题的关键．