Question

18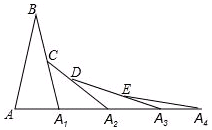．如图，已知AB=A₁B，A₁C=A₁A₂，A₂D=A₂A₃，A₃E=A₃A₄，…，以此类推，若∠B=20°，则∠A=$\frac{80°}{{2}^{n-1}}$．

Answer 1

分析 先根据等腰三角形的性质求出∠BA₁A的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA₂A₁，∠DA₃A₂及∠EA₄A₃的度数，找出规律即可得出∠A_n的度数．

解答 解：∵在△ABA₁中，∠B=20°，AB=A₁B，
∴∠BA₁A=$\frac{180°-∠B}{2}$=80°，
∵A₁A₂=A₁C，∠BA₁A是△A₁A₂C的外角，
∴∠CA₂A₁=$\frac{∠B{A}_{1}A}{2}$=40°；
同理可得，
∠DA₃A₂=20°，∠EA₄A₃=10°，
∴∠A_n=$\frac{80°}{{2}^{n-1}}$．
故答案为：$\frac{80°}{{2}^{n-1}}$．

点评 本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠CA₂A₁，∠DA₃A₂及∠EA₄A₃的度数，找出规律是解答此题的关键．