题目内容
13. 如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )
如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
分析 首先过点P作PD⊥CB于点D,利用直角三角形中30°所对边等于斜边的一半得出CD的长,再利用等腰三角形的性质求出CM的长.
解答  解:过点P作PD⊥CB于点D,
解:过点P作PD⊥CB于点D,
∵∠AOB=60°,PD⊥CB,PC=12,
∴DC=6,
∵PM=PN,MN=3,PD⊥OB,
∴MD=ND=1.5,
∴CM=6-1.5=4.5.
故选:D.
点评 此题主要考查了直角三角形中30°所对边等于斜边的一半得出CD的长以及等腰三角形的性质,得出CD的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.六边形共有几条对角线( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
8.以下列各组数据为三角形三边,不能构成三角形的是( )
| A. | 4,8,7 | B. | 3,4,7 | C. | 2,3,4 | D. | 13,12,5 |
2.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
下列结论:
(1)ac<0;
(2)抛物线顶点坐标为(1,5);
(3)3是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<3时,ax2+(b-1)x+c>0.
其中正确的个数为( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
(1)ac<0;
(2)抛物线顶点坐标为(1,5);
(3)3是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<3时,ax2+(b-1)x+c>0.
其中正确的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 已知等边三角形ABC的边长为6cm
已知等边三角形ABC的边长为6cm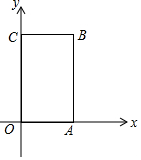 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).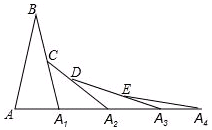 如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,…,以此类推,若∠B=20°,则∠A=$\frac{80°}{{2}^{n-1}}$.
如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,…,以此类推,若∠B=20°,则∠A=$\frac{80°}{{2}^{n-1}}$.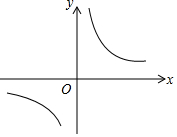 已知:Rt△ABC中,∠C=90°,∠B=60°,且BC=1,若把△ABC放入如图的直角坐标系中,使斜边AB在x轴,点C在双曲线y=$\frac{\sqrt{3}}{x}$上.
已知:Rt△ABC中,∠C=90°,∠B=60°,且BC=1,若把△ABC放入如图的直角坐标系中,使斜边AB在x轴,点C在双曲线y=$\frac{\sqrt{3}}{x}$上.