题目内容
 如图,已知二次函数y=x2-mx+m的图象与x轴的正半轴交于A、B两点,且线段AB=2,求二次函数的解析式.
如图,已知二次函数y=x2-mx+m的图象与x轴的正半轴交于A、B两点,且线段AB=2,求二次函数的解析式.考点:抛物线与x轴的交点
专题:
分析:本题是用待定系数法求二次函数的解析式,由图象与x轴交于点A(x1,0)、B(x2,0)两点,就相当于方程x2-mx+m=0两个根分别为x1,x2,由两根关系求解代入二次函数即可.
解答:解:设A(x1,0),B(x2,0),0<x2<x1,
∵二次函数y=x2-mx+m的图象与x轴的正半轴交于A、B两点,
∴x1-x2=2,
∴(x1+x2)2-4x1x2=4,
∴m2-4m=4
解得 m1=2+
,m2=2-
.
故抛物线的解析式为:y=x2-(2+
)x+2+
或y=x2-(2-
)x+2-
.
∵二次函数y=x2-mx+m的图象与x轴的正半轴交于A、B两点,
∴x1-x2=2,
∴(x1+x2)2-4x1x2=4,
∴m2-4m=4
解得 m1=2+
| 2 |
| 2 |
故抛物线的解析式为:y=x2-(2+
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了抛物线与x轴的交点.注意使用一元二次方程根与系数的关系求解关于两根的问题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )
如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )| A、45 | B、50 | C、60 | D、90 |
 如图所示,AC⊥BC,AD⊥BD,试证明:A、B、C、D在同一圆上.
如图所示,AC⊥BC,AD⊥BD,试证明:A、B、C、D在同一圆上.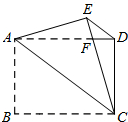 如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F,若AB=4,BC=6,求△FAC的周长和面积.
如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F,若AB=4,BC=6,求△FAC的周长和面积.