题目内容
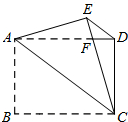如图，把矩形纸片ABCD沿对角线AC折叠，点B落在点E处，EC与AD相交于点F，若AB=4，BC=6，求△FAC的周长和面积．考点：翻折变换（折叠问题）
专题：
分析：由题意，得EC=BC=6，AE=AB=4，∠1=∠2，又由四边形ABCD是矩形，易得△AFC是等腰三角形：DF=FE，然后设DF=x，则FE=x，CF=6-x，在Rt△CDF中，DF2+CD2=CF2，即可得方程x2+42=（6-x）2，解此方程即可求得DF的长，继而求得△ACF的面积和周长．
解答：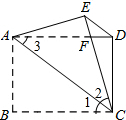
解：由题意，得EC=BC=6，AE=AB=4，∠1=∠2，
∵四边形ABCD是矩形，
∴AD∥BC，AD=BC，
∴∠1=∠3．
∴∠2=∠3．
∴AF=CF，
∴AD-AF=CE-CF，
即DF=FE．
设DF=x，则FE=x，CF=6-x，
在Rt△CDF中，DF2+CD2=CF2．
即x2+42=（6-x）2，
解得：x=
．
即DF=
，
则AF=AD-DF=
，
∵AB=4，BC=6，
∴AC=2
，
故△AFC的周长为：2
+
×2=2
+
，
S△ACF=
AF•CD=
×
×4=
．
解：由题意，得EC=BC=6，AE=AB=4，∠1=∠2，∵四边形ABCD是矩形，
∴AD∥BC，AD=BC，
∴∠1=∠3．
∴∠2=∠3．
∴AF=CF，
∴AD-AF=CE-CF，
即DF=FE．
设DF=x，则FE=x，CF=6-x，
在Rt△CDF中，DF2+CD2=CF2．
即x2+42=（6-x）2，
解得：x=
| 5 |
| 3 |
即DF=
| 5 |
| 3 |
则AF=AD-DF=
| 13 |
| 3 |
∵AB=4，BC=6，
∴AC=2
| 13 |
故△AFC的周长为：2
| 13 |
| 13 |
| 3 |
| 13 |
| 26 |
| 3 |
S△ACF=
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 3 |
| 26 |
| 3 |
点评：此题考查了矩形的性质、折叠的性质以及等腰三角形的判定与性质．此题难度适中，注意掌握折叠前后图形的对应关系，注意数形结合思想与方程思想的应用．
练习册系列答案
相关题目
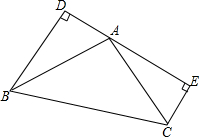如图，BD⊥DE于D，CE⊥DE于E，AD=CE=2，BD=AE=4，求AB2的值．
如图，已知二次函数y=x2-mx+m的图象与x轴的正半轴交于A、B两点，且线段AB=2，求二次函数的解析式．