题目内容
 如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )
如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )| A、45 | B、50 | C、60 | D、90 |
考点:旋转的性质
专题:计算题
分析:根据等边三角形的性质得AB=AC,∠BAC=60°,然后根据旋转的性质求解.
解答:解:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵△ADC绕点A顺时针旋转n度后到达△AEB的位置,
∴∠BAC=n°,
∴n=60°.
故选C.
∴AB=AC,∠BAC=60°,
∵△ADC绕点A顺时针旋转n度后到达△AEB的位置,
∴∠BAC=n°,
∴n=60°.
故选C.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质.

练习册系列答案
相关题目
菱形ABCD的周长为20cm,DE⊥AB,垂足为E,
=
,则下列结论正确的个数有( )
①DE=3cm;②BE=1cm;③菱形的面积为15cm2;④BD=2
cm.
| DE |
| DA |
| 3 |
| 5 |
①DE=3cm;②BE=1cm;③菱形的面积为15cm2;④BD=2
| 10 |
| A、1个 | B、2个 | C、3个 | D、4个 |
在Rt△ABC中,∠C=90°,AC=5,BC=12,则其外接圆半径为( )
| A、5 | B、12 | C、13 | D、6.5 |
 如图,直线a、b相交形成四个角,下列说法错误的是( )
如图,直线a、b相交形成四个角,下列说法错误的是( )| A、∠1与∠2互为邻补角 |
| B、∠1与∠3互为对顶角 |
| C、∠3与∠4互为邻补角 |
| D、∠3与∠2互为对顶角 |
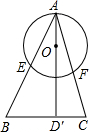 已知AD是⊙O的直径,AD′⊥BC,AB、AC分别与圆相交于E、F,那么下列等式中一定成立的是( )
已知AD是⊙O的直径,AD′⊥BC,AB、AC分别与圆相交于E、F,那么下列等式中一定成立的是( )| A、AE•BF=AF•CF |
| B、AE•AB=AO•AD′ |
| C、AE•AB=AF•AC |
| D、AE•AF=AO•AD |
某人以8折优惠价买一套服装,省了25元.买这套服装实际用了( )
| A、100元 | B、125元 |
| C、25元 | D、31.25元 |
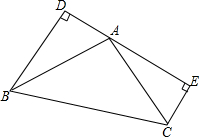 如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4,求AB2的值.
如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4,求AB2的值. 如图,已知二次函数y=x2-mx+m的图象与x轴的正半轴交于A、B两点,且线段AB=2,求二次函数的解析式.
如图,已知二次函数y=x2-mx+m的图象与x轴的正半轴交于A、B两点,且线段AB=2,求二次函数的解析式.