题目内容
10.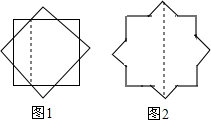 如图2的正八角形是由两个正方形(如图1)中的一个正方形绕着它的中心顺时针旋转45°形成的.
如图2的正八角形是由两个正方形(如图1)中的一个正方形绕着它的中心顺时针旋转45°形成的.(1)若正方形的边长为2+$\sqrt{2}$,则正八角形(如图2)的面积为8+$4\sqrt{2}$;
(2)请你将正八角形(如图2)剪拼成一个正方形,在图2中画出裁剪线,并画出拼接后的示意图.
分析 (1)根据题中信息可得八角形面积为2+(2+$\sqrt{2}$)2即可;
(2)根据要求画出图形即可.
解答 解:(1)∵正方形的边长为2+$\sqrt{2}$,
∴八角形面积为(2+$\sqrt{2}$)2+2=8+$4\sqrt{2}$,
故答案为:8+$4\sqrt{2}$;
(2)根据题意画图如下:
点评 此题主要考查了图形的剪拼,解此题的关键是抓住八角形与正方形的关系.

练习册系列答案
相关题目
18.2015年的世界无烟日期间,小华学习小组为了解本地区大约有多少成年人吸烟,随机调查了100个成年人,结果其中20个成年人吸烟,对于这个关于数据收集与处理的问题,下列说法正确的是( )
| A. | 调查的方式是普查 | B. | 本地区约有20%的成年人吸烟 | ||
| C. | 样本是20个吸烟的成年人 | D. | 本地区只有80个成年人不吸烟 |
15.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a2+2ab-b2=(a-b)2 | C. | (a3)2=a6 | D. | ab2+a2b=a3b2 |
19.对函数y=x3的描述:①y随x的增大而增大,②它的图象是中心对称图形,③它的自变量取值范围是x≠0.正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
 某校240名学生参加“献爱心”义务捐款活动.要求每人捐4-7元,(捐款数
某校240名学生参加“献爱心”义务捐款活动.要求每人捐4-7元,(捐款数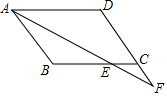 如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.