题目内容
15.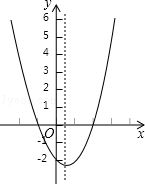 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$,y随x的增大而减小 |
分析 根据抛物线的开口方向,利用二次函数的性质判断A;
根据图形直接判断B;
根据图象,当-1<x<2时,抛物线落在x轴的下方,则y<0,进而判断C;
根据对称轴结合开口方向得出函数的增减性,从而判断D.
解答 解:A、由抛物线的开口向上,可知a>0,函数有最小值,正确,故A选项不符合题意;
B、由图象可知,对称轴为x=$\frac{1}{2}$,正确,故B选项不符合题意;
C、由图象可知,当-1<x<2时,y<0,错误,故C选项符合题意.
D、因为a>0,所以,当x<$\frac{1}{2}$时,y随x的增大而减小,正确,故D选项不符合题意;
故选:C.
点评 本题考查了二次函数的图象:y=ax2+bx+c的图象为抛物线,可利用列表、描点、连线画出二次函数的图象.也考查了二次函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
 如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
3. 如图,把图形折叠起来,它会变为下面的哪幅立体图形( )
如图,把图形折叠起来,它会变为下面的哪幅立体图形( )
 如图,把图形折叠起来,它会变为下面的哪幅立体图形( )
如图,把图形折叠起来,它会变为下面的哪幅立体图形( )| A. |  | B. |  | C. |  | D. |  |
4.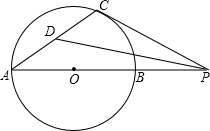 已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
 已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )| A. | 30° | B. | 20° | C. | 45° | D. | 25° |
5.下列各数中最大的数是( )
| A. | 5 | B. | $\sqrt{3}$ | C. | π | D. | -8 |
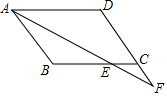 如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.
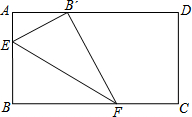 如图,在矩形ABCD中,AB=8.将矩形的一角折叠,使点B落在边AD上的B′点处,若AB′=4,则折痕EF的长度为5$\sqrt{5}$.
如图,在矩形ABCD中,AB=8.将矩形的一角折叠,使点B落在边AD上的B′点处,若AB′=4,则折痕EF的长度为5$\sqrt{5}$.