题目内容
2. 如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=$\frac{4}{x}$(x<0)上,点A和点C分别在x轴,y轴的正半轴上,DM⊥x轴于M,BN⊥x轴于N,且点A、B、C、D构成的四边形为正方形.
如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=$\frac{4}{x}$(x<0)上,点A和点C分别在x轴,y轴的正半轴上,DM⊥x轴于M,BN⊥x轴于N,且点A、B、C、D构成的四边形为正方形.(1)k的值为9;
(2)求证:△ADM≌△BAN;
(3)求点A的坐标.
分析 (1)把点B(3,3)代入双曲线y=$\frac{k}{x}$(x>0),求出k的值即可;
(2)由四边形ABCD为正方形,利用正方形的性质得到AD=AB,且∠DAB为直角,利用同角的余角相等得到一对角相等,再由一对直角相等,利用AAS即可得证;
(3)由△ADM≌△BAN得到DM=AN,AM=BN,根据B的坐标得到ON=BN=3,设A(a,0),即OA=a,由ON-OA表示出AN,即为DM,为D的纵坐标,代入反比例解析式表示出横坐标,确定出OM,由OM+OA表示出AM,根据AM=BN=3求出a的值,即可确定出A坐标.
解答 (1)解:∵点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,
∴k=3×3=9.
故答案为:9;
(2)证明:∵四边形ABCD为正方形,
∴∠DAB=90°,AD=AB,
∴∠DAM+∠BAN=90°,
∵∠MDA+∠DAM=90°,
∴∠MDA=∠BAN,
在△ADM和△BAN中,
$\left\{\begin{array}{l}∠AMD=∠BNA=90°\\∠MAD=∠BAN\\ AD=BA\end{array}\right.$,
∴△ADM≌△BAN(AAS);
(3)解:∵△ADM≌△BAN,
∴AN=DM,BN=AM,
设A(a,0),即OA=a,
∵B(3,3),
∴BN=ON=3,
∴DM=AN=ON-OA=3-a,
把y=3-a代入y=-$\frac{4}{x}$得:x=-$\frac{4}{3-a}$,即OM=$\frac{4}{3-a}$,
∴BN=AM=OM+OA=$\frac{4}{3-a}$+a=3,
解得:a=1或a=5(不合题意,舍去),
∴A(1,0).
点评 此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,全等三角形的判定与性质,正方形的性质,以及反比例函数的性质,熟练掌握判定与性质是解本题的关键.

| A. | 4x2+1 | B. | 1-4x2 | C. | 4x2-1 | D. | -4x2-1 |
| A. | a≥-2 | B. | a≤-2 | C. | a≥2 | D. | a≤2 |
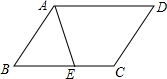 如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1cm |
 如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )| A. | 50° | B. | 60° | C. | 40° | D. | 30° |
 如图,在平行四边形ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,平行四边形ABCD的周长是14,则DM等于3.
如图,在平行四边形ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,平行四边形ABCD的周长是14,则DM等于3.