题目内容
14.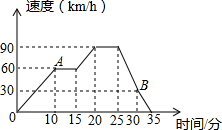 如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题:
如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题:(1)汽车从出发到最后停止共经过了多长时间?最高速度是多少?
(2)A,B两点分别表示什么?
(3)说一说速度是怎样随时间变化而变化的.
分析 (1)根据横轴得到时间,根据纵轴得到速度;
(2)写出两点的速度即可;
(3)将整个过程描述出来即可.
解答 解:(1)汽车从出发到最后停止共经过了35分钟,最高速度是90千米/时;
(2)A点表示10分时的速度为60km/h,B点表示30分时的速度是30km/h;
(3)在0到10分速度在逐渐增大;在10到15分速度保持不变;在15到20分时速度在逐渐增加;在20分到25分时速度保持不变;在25分到35分时速度在逐渐减小.
点评 考查由图象理解对应函数关系及其实际意义,需注意应首先理解函数图象的横轴和纵轴表示的量.

练习册系列答案
相关题目
6. 如图AB∥CD,∠BAE=120°,∠EDC=45°,则∠E=( )
如图AB∥CD,∠BAE=120°,∠EDC=45°,则∠E=( )
 如图AB∥CD,∠BAE=120°,∠EDC=45°,则∠E=( )
如图AB∥CD,∠BAE=120°,∠EDC=45°,则∠E=( )| A. | 105° | B. | 115° | C. | 120° | D. | 165° |
6.为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度:
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高72.2cm的课桌,它们是否配套?为什么?
| 椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
| 桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(2)现有一把高38cm的椅子和一张高72.2cm的课桌,它们是否配套?为什么?
3.某农户共摘收水蜜桃1920千克,为寻求合适的销售价格,进行了6天试销,试销情况如下:
由表中数据可知,试销期间这批水蜜桃的每天销售量y(千克)与售价x(元/千克)之间满足我们曾经学过的某种函数关系.若在这批水蜜桃的后续销售中,每天的销售量y(千克)与售价x(元/千克)之间都满足这一函数关系.
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
①若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
②该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | |
| 售价x(元/千克) | 20 | 18 | 15 | 12 | 10 | 9 |
| 销售量y(千克) | 45 | 50 | 60 | 75 | 90 | 100 |
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
①若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
②该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
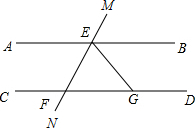 如图,直线AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠BEF,交CD于点G,若∠EFG=72°,求∠MEG的度数.
如图,直线AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠BEF,交CD于点G,若∠EFG=72°,求∠MEG的度数.
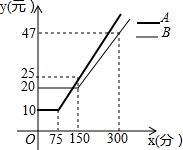 某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.
某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示. 在一次寻宝游戏中,寻宝人找到了如图所示的两个标志,点A(2,3)、B(4,1),这两个标志点到“宝藏”点的距离都是2,则“宝藏”点的坐标是(2,1)和(4,3).
在一次寻宝游戏中,寻宝人找到了如图所示的两个标志,点A(2,3)、B(4,1),这两个标志点到“宝藏”点的距离都是2,则“宝藏”点的坐标是(2,1)和(4,3).