题目内容
7.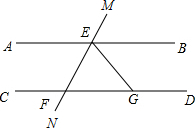 如图,直线AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠BEF,交CD于点G,若∠EFG=72°,求∠MEG的度数.
如图,直线AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠BEF,交CD于点G,若∠EFG=72°,求∠MEG的度数.
分析 根据两直线平行,同位角相等求出∠MEB=∠EFG=72°,根据两直线平行,同旁内角互补求出∠BEF,再根据角平分线的定义可得∠GEB=$\frac{1}{2}$∠FEB=54°,然后根据∠MEG=∠GEB+∠MEB计算即可得解.
解答 解:∵AB∥CD,
∴∠MEB=∠EFG=72°,
∠FEB+∠EFG=180°,即∠FEB=108°,
∵EG平分∠BEF,
∴∠GEB=$\frac{1}{2}$∠FEB=54°,
∴∠MEG=∠GEB+∠MEB=54°+72°=126°.
点评 本题考查了平行线的性质,角平分线的定义,熟记性质并准确识图是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17. 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )| A. | 8+6$\sqrt{3}$ | B. | 12$\sqrt{3}$ | C. | 19.2 | D. | 20 |
12.一次函数y=4x-2的图象可以由正比例函数y=4x的图象( )得到.
| A. | 向上平移2个单位 | B. | 向下平移4个单位 | C. | 向下平移2个单位 | D. | 向上平移4个单位 |
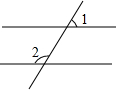 如图,已知直线AB∥CD,若∠1=2x°,∠2=(3x+30)°,则∠1=60度.
如图,已知直线AB∥CD,若∠1=2x°,∠2=(3x+30)°,则∠1=60度.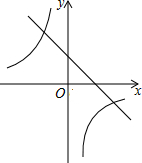 已知一次函数y1=ax+c和反比例函数y2=$\frac{b}{x}$的图象如图所示,则二次函数y3=ax2+bx+c的大致图象是( )
已知一次函数y1=ax+c和反比例函数y2=$\frac{b}{x}$的图象如图所示,则二次函数y3=ax2+bx+c的大致图象是( )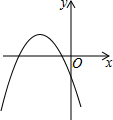
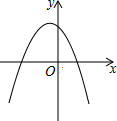
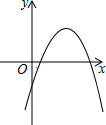
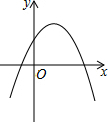
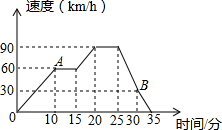 如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题:
如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题: 如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.
如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.