题目内容
5.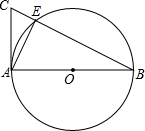 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于E点,若$\frac{OA}{CE}=\sqrt{5}$,则$\frac{AE}{AB}$=$\frac{\sqrt{5}}{5}$.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于E点,若$\frac{OA}{CE}=\sqrt{5}$,则$\frac{AE}{AB}$=$\frac{\sqrt{5}}{5}$.
分析 设CE=m,则$OA=\sqrt{5}m$,$AB=2\sqrt{5}m$,证明△ACE∽△BAE,得到$\frac{CE}{AE}=\frac{AE}{BE}$,即AE2=mEB.再根据勾股定理AB2=AE2+EB2,求出EB,即可解答.
解答 解:∵AB为⊙O的直径,
∴AE⊥BC,
设CE=m,则$OA=\sqrt{5}m$,$AB=2\sqrt{5}m$.
∵AC是⊙O的切线,
∴AC⊥AB,
∴∠CAE+∠BAE=90°,
∵∠CAE+∠C=90°
∴∠C=∠BAE,
∵∠CAB=∠AEB=90°,
∴△ACE∽△BAE,
∴$\frac{CE}{AE}=\frac{AE}{BE}$,
∴AE2=CE•EB,即AE2=mEB.
∵AB2=AE2+EB2,
∴${(2\sqrt{5}m)^2}=mEB+E{B^2}$.
∴EB2+mEB-20m2=0,
解得:EB=4m或EB=-5m(舍去).
∴AE=2m,
∴$\frac{AE}{AB}=\frac{2m}{{2\sqrt{5}m}}=\frac{{\sqrt{5}}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查了切线的性质、相似三角形的性质定理与判定定理,解决本题的关键是证明△ACE∽△BAE.

练习册系列答案
相关题目
15.下列各式经过化简后与-$\sqrt{27{x}^{3}}$不是同类二次根式的是( )
| A. | $\sqrt{27{x}^{3}}$ | B. | $\sqrt{\frac{-{x}^{3}}{27}}$ | C. | -$\frac{1}{9}$$\sqrt{3{x}^{3}}$ | D. | $\frac{\sqrt{x}}{\sqrt{3}}$ |
16.遗爱湖有5400亩,15亩=10000平方米,用科学记数法表示遗爱湖面积为( )
| A. | 8.1×105平方米 | B. | 8.1×106平方米 | C. | 3.6×105平方米 | D. | 3.6×106平方米 |
13.已知二次函数y=ax2+bx+1(a≠0)的图象的顶点在第二象限,且过点(1,0).当a-b为整数时,ab=( )
| A. | 0 | B. | $\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -2 |
14.函数y=(m-2)x+(m+1)是关于x的一次函数,那么m的取值范围是( )
| A. | m≠2 | B. | m≠-1 | C. | m=-1 | D. | m≠2且m≠-1 |