题目内容
20.若分式$\frac{x-2}{x+1}$的值为0,则x的值为( )| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 直接利用分式的值为0,则分子为0,进而得出答案.
解答 解:∵分式$\frac{x-2}{x+1}$的值为0,
∴x-2=0,x+1≠0,
解得:x=2.
故选:A.
点评 此题主要考查了分式的值为零的条件,正确把握定义是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在下列实数中,无理数是( )
| A. | $\root{3}{-27}$ | B. | -$\frac{5}{3}$ | C. | $\sqrt{0.01}$ | D. | 2π |
15.下列各式从左到右的变形属于分解因式的是( )
| A. | (a+1)(a-1)=a2-1 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2-1=x(x-$\frac{1}{x}$) |
5.在下列实数中:1.57,-6,$\sqrt{2}$,0,π,$\sqrt{4}$,-3.030030003…,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列实数中,无理数是( )
| A. | $-\frac{2}{7}$ | B. | 0 | C. | $\sqrt{8}$ | D. | 3.14 |
9.下列约分中,正确的是( )
| A. | $\frac{x^2}{x^6}=\frac{1}{x^3}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a-b}$=a+b | ||
| C. | $\frac{a+1}{{a}^{2}+1}$=$\frac{1}{a+1}$ | D. | $\frac{x+1}{{x}^{2}-2x+1}$=$\frac{1}{x+1}$ |
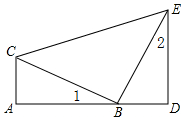 如图,已知A、B、D在同一条直线上,∠A=∠D=90°,AC=BD,∠1=∠2.
如图,已知A、B、D在同一条直线上,∠A=∠D=90°,AC=BD,∠1=∠2.
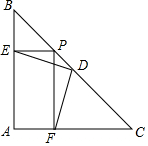 如图,已知在△ABC中,∠A=90°,AB=AC,D是BC的中点,P是BC上任意一点,且PE⊥AB于E,PF⊥AC于F,求证:DE=DF.
如图,已知在△ABC中,∠A=90°,AB=AC,D是BC的中点,P是BC上任意一点,且PE⊥AB于E,PF⊥AC于F,求证:DE=DF.