题目内容
10.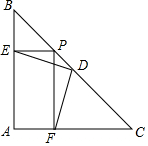 如图,已知在△ABC中,∠A=90°,AB=AC,D是BC的中点,P是BC上任意一点,且PE⊥AB于E,PF⊥AC于F,求证:DE=DF.
如图,已知在△ABC中,∠A=90°,AB=AC,D是BC的中点,P是BC上任意一点,且PE⊥AB于E,PF⊥AC于F,求证:DE=DF.
分析 连接AD,易证AF=BE,∠B=∠DAF,即可证明△BED≌△AFD,根据全等三角形对应边相等即可解题.
解答 解:连接AD,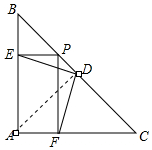
∵等腰直角△ABC中,∠BAC=90°,D为BC的中点,
∴APD=BD,∠B=∠CAD=45°,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,△BEP是等腰直角三角形,
∴AF=PE,BE=PF,
∴AF=BE,
在△BED和△AFD中,
$\left\{\begin{array}{l}{BD=AD}\\{∠B=∠DAF}\\{BE=AF}\end{array}\right.$,
∴△BED≌△AFD(SAS),
∴DE=DF.
点评 本题考查了全等三角形的判定和性质、等腰直角三角形的性质、矩形的判定和性质等知识,本题中求证△BFP≌△AEP是解题的关键,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若分式$\frac{x-2}{x+1}$的值为0,则x的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
1.把数7700000用科学记数法表示为( )
| A. | 0.77×106 | B. | 7.7×106 | C. | 0.77×107 | D. | 7.7×107 |
18.在-1,-2,-3,-4四个数中,最大的一个数是( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
5.设x表示一个一位数,y表示一个两位数,如果把x放在y的左边组成一个三位数,则这个三位数可表示为( )
| A. | xy | B. | 100x+y | C. | 10x+y | D. | x+y |
15.使分式$\frac{1}{x-1}$有意义的x的取值范围为( )
| A. | x>0 | B. | x≠-1 | C. | x≠1 | D. | 任意实数 |
18.下列各对应数是互为相反数的是( )
| A. | -(-8)与+(+8) | B. | +(+8)与+|-8| | C. | -|-8|与+(-8) | D. | -22与(-2)2 |