题目内容
15.下列各式从左到右的变形属于分解因式的是( )| A. | (a+1)(a-1)=a2-1 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2-1=x(x-$\frac{1}{x}$) |
分析 分解因式就是把一个多项式化为几个整式的积的形式.因此,要确定从左到右的变形中是否为分解因式,只需根据定义来确定.
解答 解:A、是整式的乘法,故A不符合题意;
B、x2-4=(x+2)(x-2),故B符合题意;
C、没把一个多项式化为几个整式的积的形式,故C不符合题意;
D、没把一个多项式化为几个整式的积的形式,故D不符合题意;
故选:B.
点评 本题考查了因式分解的意义.这类问题的关键在于能否正确应用分解因式的定义来判断;同时还要注意变形是否正确.

练习册系列答案
相关题目
8.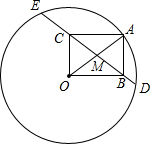 如图,⊙O的半径为10,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=6.延长BC,与⊙O分别交于D,E两点,则△OCE和△OBD的周长差等于( )
如图,⊙O的半径为10,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=6.延长BC,与⊙O分别交于D,E两点,则△OCE和△OBD的周长差等于( )
 如图,⊙O的半径为10,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=6.延长BC,与⊙O分别交于D,E两点,则△OCE和△OBD的周长差等于( )
如图,⊙O的半径为10,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=6.延长BC,与⊙O分别交于D,E两点,则△OCE和△OBD的周长差等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | 1 | D. | $\frac{6}{5}$ |
3.(1+3a)(3a-1)=( )
| A. | 3a2-1 | B. | 1-9a2 | C. | 9a2-1 | D. | a2-3 |
10.若(x-3)(x+2)=x2+mx-6,则m的值是( )
| A. | -5 | B. | 5 | C. | -1 | D. | 1 |
20.若分式$\frac{x-2}{x+1}$的值为0,则x的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
4.下列各数中,为负数的是( )
| A. | 0 | B. | -2 | C. | 1 | D. | 0.001 |
5.设x表示一个一位数,y表示一个两位数,如果把x放在y的左边组成一个三位数,则这个三位数可表示为( )
| A. | xy | B. | 100x+y | C. | 10x+y | D. | x+y |
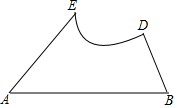 有一个三角形工件△ABC,根据安装需要,把∠C切掉了,如图,现在要在工件上画出一条线段,使它是∠C的平分线在阴影面留下的那部分.
有一个三角形工件△ABC,根据安装需要,把∠C切掉了,如图,现在要在工件上画出一条线段,使它是∠C的平分线在阴影面留下的那部分.