题目内容
5.探究:如图1,锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD、CE,试猜想BD与CE的大小关系,并说明理由.应用:如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45°,则BD的长为$\sqrt{107}$cm.

分析 (1)首先根据等式的性质证明∠EAC=∠BAD,则根据SAS即可证明△EAC≌△BAD,根据全等三角形的性质即可证明;
(2)在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC,证明△EAC≌△BAD,证明BD=CE,然后在直角三角形BCE中利用勾股定理即可求解.
解答 解:(1)BD=CE.
理由是:∵∠BAE=∠CAD,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
$\left\{\begin{array}{l}{AE=AB}\\{∠EAC=∠BAD}\\{AC=AD}\end{array}\right.$,
∴△EAC≌△BAD,
∴BD=CE;
(2)如图2,在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC.
∵∠ACD=∠ADC=45°,
∴AC=AD,∠CAD=90°,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
$\left\{\begin{array}{l}{AE=AB}\\{∠EAC=∠BAD}\\{AC=AD}\end{array}\right.$,
∴△EAC≌△BAD,
∴BD=CE.
∵AE=AB=7,
∴BE=$\sqrt{{7}^{2}+{7}^{2}}$=7$\sqrt{2}$,∠AEC=∠AEB=45°,
又∵∠ABC=45°,
∴∠ABC+∠ABE=45°+45°=90°,
∴EC=$\sqrt{B{E}^{2}+B{C}^{2}}$=$\sqrt{(7\sqrt{2})^{2}+{3}^{2}}$=$\sqrt{107}$,
∴BD=CE=$\sqrt{107}$.
故答案为:$\sqrt{107}$.
点评 本题考查了全等三角形的判定与性质,正确理解题目之间的联系,构造(1)中的全等三角形是解决本题的关键.

| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
信息一:可供选择的树苗有雪松、香樟,垂柳三种,并要求购买雪松、香樟的数量相等.
信息二:如下表:设购买雪松,垂柳分别为x株、y株.
| 树苗 | 每株树苗批发价格(元) | 两年后每株树苗对空气的净化指数 |
| 雪松 | 30 | 0.4 |
| 香樟 | 20 | 0.1 |
| 垂柳 | P | 0.2 |
(2)当每株垂柳的批发价P等于30元时,要使这400株树苗两年后对该住宅小区的空气净化指数不低于90,应
怎样安排这三种树苗的购买数量,才能使购买树苗的总费用最低?最低的总费用是多少元?
(3)当每株垂柳批发价格P(元)与购买数量y(株)之间存在关系P=30-0.05y时,求购买树苗的总费用W(元)与购买雪松数量x(株)之间的函数关系式(不要求写出自变量的取值范围),并求出购买树苗总费用的最大值.
| A. | 由7-x=13,得x=13-7 | B. | 由5x=4x+8,得5x-4x=8 | ||
| C. | 由$\frac{1}{2}$x=1,得x=$\frac{1}{2}$ | D. | 由7x+6=5x,得7x-5x=6 |
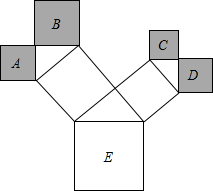 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是4、6、3、4,则最大正方形E的面积是17.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是4、6、3、4,则最大正方形E的面积是17.