题目内容
17.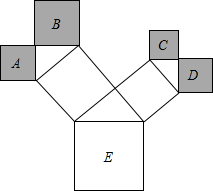 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是4、6、3、4,则最大正方形E的面积是17.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是4、6、3、4,则最大正方形E的面积是17.
分析 根据正方形的面积公式,运用勾股定理可以证明:四个小正方形的面积和等于最大正方形的面积,由此即可解决问题.
解答 解:如图记图中两个正方形分别为P、Q.
根据勾股定理得到:C与D的面积的和是Q的面积;A与B的面积的和是P的面积;而P,Q的面积的和是E的面积,
即A、B、C、D的面积之和为E的面积,
∴正方形E的面积=4+6+3+4=17,
故答案为:17.
点评 本题考查了勾股定理的应用.能够发现正方形A,B,C,D的边长正好是两个直角三角形的四条直角边,根据勾股定理最终能够证明正方形A,B,C,D的面积和即是最大正方形的面积.

练习册系列答案
相关题目
20.-2的相反数是( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
2. 如图,AB为⊙O的直径,弦CD⊥AB,E为弧BC上一点,若∠CEA=28°,则∠ABD=( )
如图,AB为⊙O的直径,弦CD⊥AB,E为弧BC上一点,若∠CEA=28°,则∠ABD=( )
 如图,AB为⊙O的直径,弦CD⊥AB,E为弧BC上一点,若∠CEA=28°,则∠ABD=( )
如图,AB为⊙O的直径,弦CD⊥AB,E为弧BC上一点,若∠CEA=28°,则∠ABD=( )| A. | 14° | B. | 28° | C. | 56° | D. | 80° |
9.暑假期间,读大学的王刚同学回家帮助父母开了一家冷饮销售摊点,他发现销售某种冷饮每天的成本C(元)与销售数量t(个)可以近似地表示为C=3t+100,为了每天获取最大利润,他经过调查,得到销售数量t与销售单价x之间有如下关系:
(1)试用已学过的函数刻画销售数量t与销售单价x之间的关系;
(2)试求每天的利润P(元)与销售单价x的函数关系;(每天利润=销售单价×销售数量-每天成本)
(3)王刚的弟弟认为“定价越高获利越多”,你同意他的观点吗?请求出每天的最大利润.
| 销售单价x/元 | 4 | 5 | 6 | 7 | 8 |
| 销售数量t/件 | 120 | 100 | 80 | 60 | 40 |
(2)试求每天的利润P(元)与销售单价x的函数关系;(每天利润=销售单价×销售数量-每天成本)
(3)王刚的弟弟认为“定价越高获利越多”,你同意他的观点吗?请求出每天的最大利润.
6.x是9的平方根,y是64的立方根,则x+y的值为( )
| A. | 3 | B. | 7 | C. | 3,7 | D. | 1,7 |
