题目内容
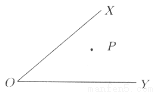
如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.
 见解析
【解析】【解析】
如图所示,分别以直线OX、OY为对称轴,作点P的对称点与,
连接,分别交OX于点M,交OY于点N,则PM+MN+NP最短.
见解析
【解析】【解析】
如图所示,分别以直线OX、OY为对称轴,作点P的对称点与,
连接,分别交OX于点M,交OY于点N,则PM+MN+NP最短.
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
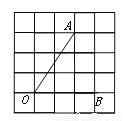
如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是( )
A.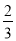 B.
B.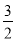 C.
C.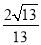 D.
D.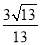
 D.
【解析】
试题分析:在直角△OAC中,OC=2,AC=3,则OA===,则sin∠AOB===.故选D.
D.
【解析】
试题分析:在直角△OAC中,OC=2,AC=3,则OA===,则sin∠AOB===.故选D. 如图是经过轴对称变换后所得的图形,与原图形相比
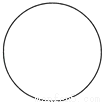
A.形状没有改变,大小没有改变 B.形状没有改变,大小有改变
C.形状有改变,大小没有改变 D.形状有改变,大小有改变
 A
【解析】
试题分析:∵轴对称变换不改变图形的形状与大小,
∴与原图形相比,形状没有改变,大小没有改变。
故选A。
A
【解析】
试题分析:∵轴对称变换不改变图形的形状与大小,
∴与原图形相比,形状没有改变,大小没有改变。
故选A。 若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是( )
A. 2 B. 4 C. 6 D. 8
 C
【解析】试题分析:根据题意可得A=(2-1)(2+1)(22+1)(24+1)(28+1)
=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1
根据21=2;22=4;23=8;24=16;25=32;···因此可由16÷4=4,所以216的末位为6,则216-1的末位为5.
...
C
【解析】试题分析:根据题意可得A=(2-1)(2+1)(22+1)(24+1)(28+1)
=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1
根据21=2;22=4;23=8;24=16;25=32;···因此可由16÷4=4,所以216的末位为6,则216-1的末位为5.
... 下列计算正确的是( )
A. -bx2y3÷2xy3=-3x B. (-xy2)2÷(-x2y)=-y3
C. (-2x2y2)3÷(-xy)3=-2x3y3 D. -(-a3b2)÷(-a2b2)=a4
 B
【解析】选项A,-bx2y3÷2xy3=-bx;选项B,原式==-y3;选项C,(-2x2y2)3÷(-xy)3=8x3y3;选项D,-(-a3b2)÷(-a2b2)=-a.故选B.
B
【解析】选项A,-bx2y3÷2xy3=-bx;选项B,原式==-y3;选项C,(-2x2y2)3÷(-xy)3=8x3y3;选项D,-(-a3b2)÷(-a2b2)=-a.故选B. 如图(1)、图(2)都是轴对称图形,图(1)有 条对称轴,图(2)有 条对称轴
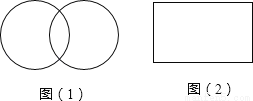
 2,2
【解析】根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴.依此对连心园、长方形图形进行判断
2,2
【解析】根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴.依此对连心园、长方形图形进行判断 在等边△ABC中,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长为 ( )
A. 2a B. 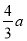 C. 1.5a D. a
C. 1.5a D. a
 C
【解析】【解析】
△ABC是等边三角形,由折叠可知,AD=BD=0.5AB=0.5a,易得△ADE是等边三角形.故周长是1.5a。故选 C.
C
【解析】【解析】
△ABC是等边三角形,由折叠可知,AD=BD=0.5AB=0.5a,易得△ADE是等边三角形.故周长是1.5a。故选 C. 如果直线a∥b,b∥c,那么a∥c。这个推理的依据是( )
A. 等量代换; B. 平行公理;
C. 两直线平行,同位角相等; D. 平行于同一直线的两条直线平行。
 D
【解析】试题分析:在同一平面内,平行于同一条直线的两直线平行,故本题选D.
D
【解析】试题分析:在同一平面内,平行于同一条直线的两直线平行,故本题选D. 在△ABC中,∠C=90°,a=5,c=17,用科学计算器求∠A约等于 ( )
A. 17.6° B. 17°6′ C. 17°16′ D. 17.16°
 A
【解析】试题解析:sinA=,
A=sin-10.294=17.6°,
故选A.
A
【解析】试题解析:sinA=,
A=sin-10.294=17.6°,
故选A. 
